
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
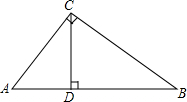 如图所示,AC⊥BC,CD⊥AB,AC=5cm,BC=12cm,AB=13cm,则点A到BC的距离是5cm,点C到AB的距离是$\frac{60}{13}$cm.
如图所示,AC⊥BC,CD⊥AB,AC=5cm,BC=12cm,AB=13cm,则点A到BC的距离是5cm,点C到AB的距离是$\frac{60}{13}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
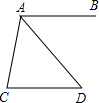 如图,AB∥CD,AD平分∠BAC,且∠C=80°,则∠D等于多少度?
如图,AB∥CD,AD平分∠BAC,且∠C=80°,则∠D等于多少度?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
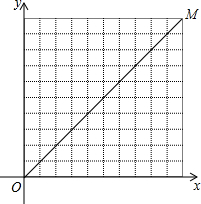 如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.如果抛物线经过图中的三个格点,那么以这三个格点为顶点的三角形称为该抛物线的“内接格点三角形”.设对称轴平行于y轴的抛物线与网格对角线OM的两个交点为A,B,其顶点为C,如果△ABC是该抛物线的内接格点三角形,AB=3$\sqrt{2}$,且点A,B,C的横坐标xA,xB,xC满足xA<xC<xB,那么符合上述条件的抛物线条数是( )
如图,在10×10的网格中,每个小方格都是边长为1的小正方形,每个小正方形的顶点称为格点.如果抛物线经过图中的三个格点,那么以这三个格点为顶点的三角形称为该抛物线的“内接格点三角形”.设对称轴平行于y轴的抛物线与网格对角线OM的两个交点为A,B,其顶点为C,如果△ABC是该抛物线的内接格点三角形,AB=3$\sqrt{2}$,且点A,B,C的横坐标xA,xB,xC满足xA<xC<xB,那么符合上述条件的抛物线条数是( )| A. | 7 | B. | 8 | C. | 14 | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
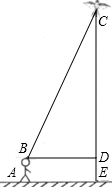 身高1.6米的小明想利用“勾股定理”测得下图风筝CE的高度,于是他测得BD的长度为25米,并根据手中剩余线的长度计算出风筝线BC的长为65米.求风筝的高度CE.
身高1.6米的小明想利用“勾股定理”测得下图风筝CE的高度,于是他测得BD的长度为25米,并根据手中剩余线的长度计算出风筝线BC的长为65米.求风筝的高度CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com