
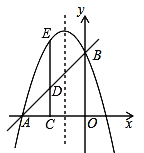
����Ŀ����ֱ֪��y=x+3��x���ڵ�A����y���ڵ�B��������y=![]() x2+bx+c������A��B��
x2+bx+c������A��B��
��1���������߽���ʽ��
��2����C��m��0�����߶�OA�ϣ���C����A��O���غϣ���CD��OA��AB�ڵ�D�����������ڵ�E����DE=![]() AD����m��ֵ��
AD����m��ֵ��
��3����M���������ϣ���N�������ߵĶԳ����ϣ��ڣ�2���������£��Ƿ�����Ե�D��B��M��NΪ������ı���Ϊƽ���ı��Σ������ڣ��������N�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=![]() x2
x2![]() 2x+3��2��-2��3��������
2x+3��2��-2��3��������![]() 1��
1��![]() 2����
2����![]() 1��0��
1��0��
����������������1������ֱ��![]() ��
��![]() ���
���![]() ��Ľ������꣬���ô���ϵ�����������ߵĽ���ʽ��
��Ľ������꣬���ô���ϵ�����������ߵĽ���ʽ��
��2�����ݵ�C�ĺ�����Ϊm�ɵ�D��E�ĺ����궼��m�����ݽ���ʽ��ʾ�������꣬����Ǧֱ�߶�DE�ij������ù��ɶ����ã�![]() ��������֪��ʽ�ɵ�m��ֵ��
��������֪��ʽ�ɵ�m��ֵ��
��3�������������
����BCΪһ�ߣ���ͼ1��֤��![]() ��
��![]() ����
����![]() �ɵ�
�ɵ�![]()
�ڵ�BDΪ�Խ���ʱ����ͼ2��M�������ߵĶ��㣬N�ǶԳ�����x��Ľ��㣬��ʱ![]()
��⣺(1)��x=0ʱ��y=3��
��B(0,3)��
��y=0ʱ��x+3=0��
x=3��
��A(3,0)��
��A(3,0),B(0,3)����������![]() �еã�
�еã�
![]() ��ã�
��ã�![]()
�������ߵĽ���ʽΪ��![]()
(2)��CD��OA,C(m,0)��
��![]()
��![]()
��AC=m+3,CD=m+3,
�ɹ��ɶ����ã�![]()
��![]()
��![]()
![]()
(m+3)(m+2)=0��
m1=3(��),m2=2��
(3)���ڣ������������
����BCΪһ�ߣ���ͼ1����Գ�����x�ύ�ڵ�G��
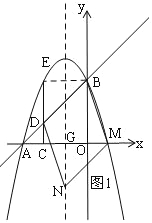
��C(2,0)��
��D(2,1),E(2,3),
��E��B���ڶԳ���Գƣ�
��BE��x�ᣬ
���ı���DNMB��ƽ���ı��Σ�
��BD=MN,BD��MN��
��![]()
���EDB�ա�GNM��
��NG=ED=2��
��N(1,2)��
�ڵ�BDΪ�Խ���ʱ����ͼ2��
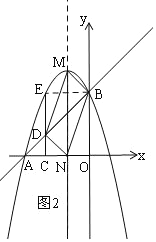
M�������ߵĶ��㣬N�ǶԳ�����x��Ľ��㣬��ʱ�ı���BMDN��ƽ���ı��Σ�
��ʱN(1,0)��
��������,��N������Ϊ(1,2)��(1,0).



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��y=4��x�뷴��������y=![]() ��m��0��x��0����ͼ����A��B���㣬�ҵ�A�ĺ�����Ϊ1����x�ᣬy��ֱ��ཻ��C��D���㣮
��m��0��x��0����ͼ����A��B���㣬�ҵ�A�ĺ�����Ϊ1����x�ᣬy��ֱ��ཻ��C��D���㣮
��1������һ������B�����ꣻ
��2�����ú���ͼ�������x�IJ���ʽ4��x��![]() �Ľ⼯��
�Ľ⼯��
��3����������AOB�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����0��2��4��8��12��18�����е��������ż����ֱ��ô���ʽ![]() ��
��![]() ��ʾ�����1����Ϊ
��ʾ�����1����Ϊ![]() ����2����Ϊ
����2����Ϊ![]() ����3����Ϊ
����3����Ϊ![]() ���������8������ֵ��_____������������һ��
���������8������ֵ��_____������������һ��![]() ��ԭ������������Դ������е���Ϊ����������������Ծ����1��ʱ����
��ԭ������������Դ������е���Ϊ����������������Ծ����1��ʱ����![]() ��ԭ�㣬��Ϊ
��ԭ�㣬��Ϊ![]() ����2���
����2���![]() ������2����λ����Ϊ
������2����λ����Ϊ![]() ����ʱ��
����ʱ��![]() ��ʾ����Ϊ-2����3���
��ʾ����Ϊ-2����3���![]() ������4����λ����Ϊ
������4����λ����Ϊ![]() ����
����![]() ��ʾ����Ϊ2�������˹�����Ծ����
��ʾ����Ϊ2�������˹�����Ծ����![]() ��ʾ����Ϊ_______��
��ʾ����Ϊ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��֪![]() �Ķ���
�Ķ���![]() ,
,![]() ,��
,��![]() ��
��![]() �����������,�����²�����ͼ:���Ե�
�����������,�����²�����ͼ:���Ե�![]() ΪԲ�ġ��ʵ�����Ϊ�뾶����,�ֱ�
ΪԲ�ġ��ʵ�����Ϊ�뾶����,�ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ,
,![]() ���ڷֱ��Ե�
���ڷֱ��Ե�![]() ,
,![]() ΪԲ�ġ�����
ΪԲ�ġ�����![]() �ij�Ϊ�뾶����,������
�ij�Ϊ�뾶����,������![]() �ڽ��ڵ�
�ڽ��ڵ�![]() ����������
����������![]() ,����
,����![]() �ڵ�
�ڵ�![]() .���
.���![]() ������Ϊ( )
������Ϊ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ģ�ͣ�����ѳ�Ϊ�Ϸʳ��в�֮һ����Ҫ�����ھ�סͣ��λ���㣬ͣ����Դ�ṹ��ʧ�⣬���ij����������ȵ�.��ͼ������ʦ�ij���ǽƽ��ͣ�ŵ�ƽ��ʾ��ͼ��������ǽһ��OB��ǽMNƽ���Ҿ���Ϊ0.8�ף���֪С�������ſ�AOΪ 1.2 �ף������ŴǶȡ�AOBΪ40��ʱ�������Ƿ������ǽ����˵������.���ο����ݣ�sin 40���0.64��cos 40���0.77��tan 40���0.84��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �ϲ��ֵ�ĺ�����
�ϲ��ֵ�ĺ�����![]() ��������
��������![]() �Ķ�Ӧֵ���±���
�Ķ�Ӧֵ���±���
x | �� | ��2 | ��1 | 0 | 1 | 2 | �� |
y | �� | 0 | 4 | 6 | 6 | 4 | �� |
С�Ϲ۲��ϱ����ó�������ۣ�����������x���һ������Ϊ��3��0���� �ں���![]() �����ֵΪ6���������ߵĶԳ�����
�����ֵΪ6���������ߵĶԳ�����![]() �����ڶԳ�����࣬y��x���������������ȷ��( )
�����ڶԳ�����࣬y��x���������������ȷ��( )
A. �٢� B. �٢� C. �٢ڢ� D. �٢���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
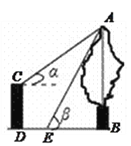
����Ŀ����ͼ��CD��һ��Ϊ4��ƽ̨��AB����CD�ײ���ƽ��һ��������ƽ̨��C��������A�������![]()
![]() ����ƽ̨�ײ������ķ���ˮƽǰ��3�����E���ڵ�E���������A�������
����ƽ̨�ײ������ķ���ˮƽǰ��3�����E���ڵ�E���������A�������![]() ��������AB(�����������).
��������AB(�����������).
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������о���������Ѫ����Ũ���������˶���о�ƣ�͵���Ҫԭ���˶�Աδ�˶�ʱ������Ѫ����Ũ��ˮƽͨ����40mg/L���£����Ѫ����Ũ�Ƚ���50mg/L���£��˶�Ա�ͻ���������ƣ�ͣ��������й����߸���ʵ�����ݣ�������һ��ͼ������ӳ���˶�Ա���и�ǿ���˶�������Ѫ����Ũ����ʱ��仯���仯�ĺ�����ϵ.
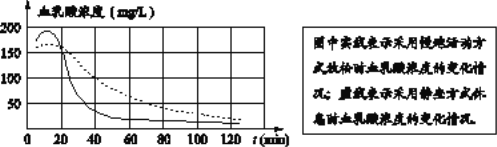
����������ȷ����
A. �˶���40minʱ���������ܻ��ʽ����ʱ��Ѫ����Ũ������þ�����ʽ��Ϣʱ��Ѫ����Ũ����ͬ
B. �˶�Ա��ǿ���˶������Ѫ����Ũ�ȴ�ԼΪ350mg/L
C. �˶�Ա����������˶���Ϊ�˸���ﵽ����ƣ�͵�Ч����Ӧ�ò������ܻ��ʽ������
D. �������ܻ��ʽ����ʱ���˶�Ա��������80min����ܻ�������ƣ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AD��6��AE��BD������ΪE��DE��3BE����P��Q�ֱ���BD��AD �ϣ���AP��PQ����СֵΪ��
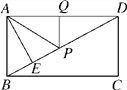
A. 2![]() B.
B. ![]() C. 2
C. 2![]() D. 3
D. 3![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com