练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】根据研究，人体内血乳酸浓度升高是运动后感觉疲劳的重要原因，运动员未运动时，体内血乳酸浓度水平通常在40mg/L以下；如果血乳酸浓度降到50mg/L以下，运动员就基本消除了疲劳，体育科研工作者根据实验数据，绘制了一副图象，它反映了运动员进行高强度运动后，体内血乳酸浓度随时间变化而变化的函数关系.

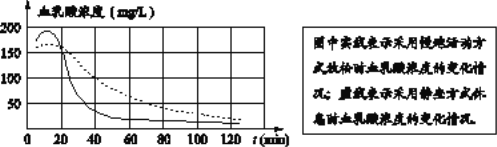
    下列叙述正确的是

    A. 运动后40min时，采用慢跑活动方式放松时的血乳酸浓度与采用静坐方式休息时的血乳酸浓度相同

    B. 运动员高强度运动后最高血乳酸浓度大约为350mg/L

    C. 运动员进行完剧烈运动，为了更快达到消除疲劳的效果，应该采用慢跑活动方式来放松

    D. 采用慢跑活动方式放松时，运动员必须慢跑80min后才能基本消除疲劳

    【答案】C

    【解析】故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校在八年级举行“汉字听写”比赛，每位学生听写汉字39个，比赛结束后随机抽查30名学生的听写汉字的正确字数如下：

    2

    9

    17

    24

    33

    5

    12

    19

    26

    34

    7

    14

    20

    26

    36

    15

    22

    26

    39

    31

    22

    27

    39

    22

    28

    23

    23

    31

    30

    28

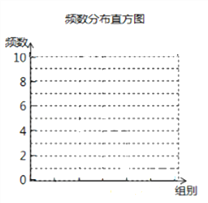
    对这30个数据按组距8进行分组，并统计整理．

    （1）请完成下面频数分布统计表；

    组别

    正确字数x

    频数

    A

    0≤x＜8

    B

    8≤x＜16

    C

    16≤x＜24

    D

    24≤x＜32

    E

    32≤x＜40

    （2）在上图中请画出频数分布直方图；

    （3）若该校八年级学生共有1200人，如果听写正确的个数少于24个定为不合格，请你估计该校八年级本次比赛听写不合格的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

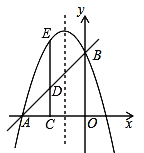
    【题目】已知直线y=x+3交x轴于点A，交y轴于点B，抛物线y=x2+bx+c经过点A，B．

    （1）求抛物线解析式；

    （2）点C（m，0）在线段OA上（点C不与A，O点重合），CD⊥OA交AB于点D，交抛物线于点E，若DE=AD，求m的值；

    （3）点M在抛物线上，点N在抛物线的对称轴上，在（2）的条件下，是否存在以点D，B，M，N为顶点的四边形为平行四边形？若存在，请求出点N的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】“金牛绿道行“活动需要租用、两种型号的展台,经前期市场调查发现,用元租用的型展台的数量与用元租用的型展台的数量相同,且每个型展台的价格比每个型展台的价格少元.

    (1)求每个型展台、每个型展台的租用价格分别为多少元(列方程解应用题)；

    (2)现预计投入资金至多元,根据场地需求估计,型展台必须比型展台多个,问型展台最多可租用多少个.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

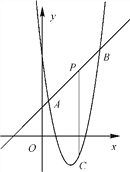
    【题目】如图，直线y＝x＋2与抛物线y＝ax2＋bx＋6相交于A(， )和B(4，m)，点P是线段AB上异于A、B的动点，过点P作PC⊥x轴，交抛物线于点C.

    (1)求抛物线的表达式；

    (2)是否存在这样的点P，使线段PC的长有最大值？若存在，求出这个最大值，若不存在，请说明理由；

    (3)当△PAC为直角三角形时，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明在暑期社会实践活动中，以每千克0．8元的价格从批发市场购进若干千克瓜到市场上去销售，销售了40kg西瓜之后，余下的每千克降价0．4元，全部售完销售金额与售出西瓜的千克数之间的关系如图所示，小明这次卖瓜赚________元．

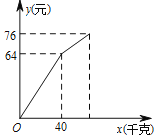
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形ABCD中，AB＝4，AD＝3，E为对角线BD上一个动点，以E为直角顶点，AE为直角边作等腰Rt△AEF，A、E、F按逆时针排列．当点E从点B运动到点D时，点F的运动路径长为___________.

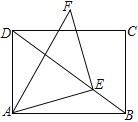
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】给出如下定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称该四边形为勾股四边形．

    （1）以下四边形中，是勾股四边形的为 ．（填写序号即可）

    ①矩形；②有一个角为直角的任意凸四边形；③有一个角为60°的菱形．

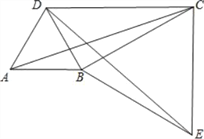
    （2）如图，将△ABC绕顶点B按顺时针方向旋转60°得到△DBE，∠DCB=30°，连接AD，DC，CE．

    ①求证：△BCE是等边三角形；

    ②求证：四边形ABCD是勾股四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】关于的方程有两个不相等的实数根．

    求实数的取值范围；

    是否存在实数，使方程的两个实数根之和等于两实数根之积的算术平方根？若存在，求出的值；若不存在，说明理由．

    查看答案和解析>>

    同步练习册答案