
【题目】已知:![]() 为
为![]() 的直径,
的直径,![]() 为圆弧上一点,
为圆弧上一点,![]() 垂直于过
垂直于过![]() 点的切线,垂足为
点的切线,垂足为![]() ,
,![]() 的延长线交直线
的延长线交直线![]() 于点
于点![]() .
.![]() ,垂足为点
,垂足为点![]() .
.
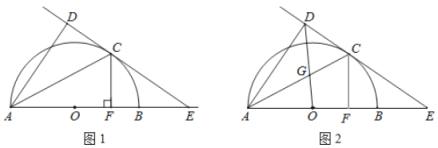
(1)如图1,求证:![]() ;
;
(2)如图2,若![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,且
,且![]() 时,求
时,求![]() 的长度.
的长度.
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,AB⊥AC,DC⊥AC,∠B=∠D,![]() ,
,![]() ,
,![]() ,点E,F分别是BC,AD的中点.
,点E,F分别是BC,AD的中点.
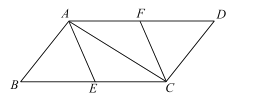
(1)求证:![]() ;
;
(2)当![]() 与
与![]() 满足什么数量关系时,四边形
满足什么数量关系时,四边形![]() 是正方形?请证明.
是正方形?请证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李在景区销售一种旅游纪念品,已知每件进价为![]() 元,当销售单价定为
元,当销售单价定为![]() 元时,每天可以销售
元时,每天可以销售![]() 件.市场调查反映:销售单价每提高
件.市场调查反映:销售单价每提高![]() 元,日销量将会减少
元,日销量将会减少![]() 件,物价部门规定:销售单价不能超过
件,物价部门规定:销售单价不能超过![]() 元,设销售单价为
元,设销售单价为![]() (元).
(元).
(1)要使日销售利润为![]() 元,销售单价应定为多少元;
元,销售单价应定为多少元;
(2)求日销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)的函数关系式,当
(元)的函数关系式,当![]() 为何值时,日销售利润最大,并求出最大利润.
为何值时,日销售利润最大,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
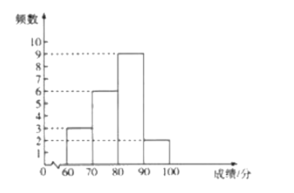
【题目】随着“全民健身”时代的到来,健身已经成为推广文明生活的重要途径,成为国民增强身体素质和提高身体免疫力的重要方法.某校为促进学生对健身知识的了解,在七、八年级中开展了“健身知识知多少”的竞赛活动.现从该校七、八年级中各随机抽取![]() 名学生的竞赛成绩进行整理描述和分析,下面给出了部分信息:
名学生的竞赛成绩进行整理描述和分析,下面给出了部分信息:
a.七年级![]() 名学生成绩为:
名学生成绩为:
![]()
![]()
b.八年级![]() 名学生成绩的频数分布直方图如图:
名学生成绩的频数分布直方图如图:
c.八年级成绩在![]() 这一组的是:
这一组的是:
![]()
d.七、八年级成绩的平均数、中位数、众数如下:
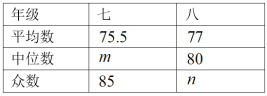
根据以上信息,回答下列问题:
(1)表中![]() , .
, .
(2)一名七年级学生和一名八年级学生发生了争论.均认为本年级的成绩更好.请你写出他们的理由:
七年级学生理由: ;
八年级学生理由: ;
(3)若该校七、八年级各有![]() 名学生.请估计该校七、八年级此次竞赛成绩优秀
名学生.请估计该校七、八年级此次竞赛成绩优秀![]() 的学生共有多少人.
的学生共有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ABD都是⊙O的内接三角形,圆心O在边AB上,边AD分别与BC,OC交于E,F两点,点C为![]() 的中点.
的中点.
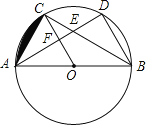
(1)求证:OF∥BD;
(2)若![]() ,且⊙O的半径R=6cm.①求证:点F为线段OC的中点; ②求图中阴影部分(弓形)的面积.
,且⊙O的半径R=6cm.①求证:点F为线段OC的中点; ②求图中阴影部分(弓形)的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线L1:![]() 过点C(0,﹣3),与抛物线L2:
过点C(0,﹣3),与抛物线L2:![]() 的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.
的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.
(1)求抛物线L1对应的函数表达式;
(2)若以点A、C、P、Q为顶点的四边形恰为平行四边形,求出点P的坐标;
(3)设点R为抛物线L1上另一个动点,且CA平分∠PCR,若OQ∥PR,求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
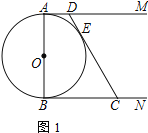
【题目】已知![]() 是
是![]() 的直径,
的直径,![]() 和
和![]() 是
是![]() 的两条切线,
的两条切线,![]() 与
与![]() 相切于点
相切于点![]() ,分别交
,分别交![]() 、
、![]() 于
于![]() 、
、![]() 两点
两点
(1)如图1,求证:![]()
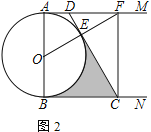
(2)如图2,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,求图中阴影部分的面积
,求图中阴影部分的面积
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 y=ax2+bx+c,其中 y 与 x 的部分对应值如表:
x | -2 | -1 | 0.5 | 1.5 |
y | 5 | 0 | -3.75 | -3.75 |
下列结论正确的是( )
A.abc<0B.4a+2b+c>0
C.若 x<-1 或 x>3 时,y>0D.方程 ax2+bx+c=5 的解为 x1=-2,x2=3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com