
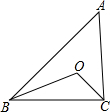
 如图,△ABC中,O是∠ABC和∠ACB的角平分线的交点,若∠A=40°,则∠BOC=110°.
如图,△ABC中,O是∠ABC和∠ACB的角平分线的交点,若∠A=40°,则∠BOC=110°. 分析 求出∠ABC+∠ACB的度数,根据平分线的定义得出∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,求出∠OBC+∠OCB的度数,根据三角形内角和定理求出即可.
解答 解:∵∠A=40°,
∴∠ABC+∠ACB=180°-∠A=140°,
∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=70°,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-70°=110°,
故答案为:110.
点评 本题考查了三角形内角和定理,角平分线定义的应用,注意:三角形的内角和等于180°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
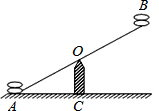 如图是跷跷板示意图,横板AB绕中点O上下转动,立柱OC与地面垂直,当横板AB的A端着地时,测得∠OAC=α,则在玩跷跷板时,横板AB绕点O上下转动的最大角度为2α°.
如图是跷跷板示意图,横板AB绕中点O上下转动,立柱OC与地面垂直,当横板AB的A端着地时,测得∠OAC=α,则在玩跷跷板时,横板AB绕点O上下转动的最大角度为2α°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x+y=18 | B. | x+y=36 | C. | 4x+2y=36 | D. | 2x+4y=36 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
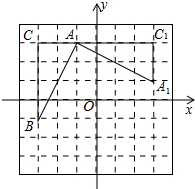 如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.
如图,在平面直角坐标系中,有一Rt△ABC,且A(-1,3),B(-3,-1),C(-3,3),已知△A1AC1是由△ABC旋转得到的.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{37}$ | B. | $\sqrt{13}$ | C. | $\sqrt{37}$、$\sqrt{13}$ | D. | $\sqrt{37}$、$\sqrt{13}$、5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
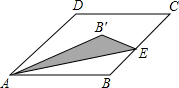 如图,已知在周长为20的菱形ABCD中,∠C=45°,点E是线段BC上一点,将△ABE沿AE所在直线翻折,使点B落在B′上,则在点E沿B→C→D运动的过程中,点B′运动的路径长是$\frac{5π}{4}$.
如图,已知在周长为20的菱形ABCD中,∠C=45°,点E是线段BC上一点,将△ABE沿AE所在直线翻折,使点B落在B′上,则在点E沿B→C→D运动的过程中,点B′运动的路径长是$\frac{5π}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com