
ЁОЬтФПЁПФГаЃЮЊСЫЗсИЛЭЌбЇУЧЕФПЮЭтЛюЖЏЃЌОіЖЈИјШЋаЃ20ИіАрУПАрХф4ИБЦЙХвЧђХФКЭШєИЩЦЙХвЧђЃЌСНМвЬхг§гУЦЗЩЬЕъЖдЭЌвЛПюЦЙХвЧђХФКЭЦЙХвЧђЭЦГіШУРћЛюЖЏЃЌМзЩЬЕъТђвЛИБЦЙХвЧђХФЫЭ10ИіЦЙХвЧђЃЌввЩЬЕъЫљгаЩЬЦЗОљДђОХелЃЈАДБъМлЕФ90ЃЅЃЉЯњЪлЃЌвбжЊ2ИБЦЙХвЧђХФКЭ10ИіЦЙХвЧђ110дЊЃЌ3ИБЦЙХвЧђХФКЭ20ИіЦЙХвЧђ170дЊЁЃ
ЧыНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓУПИБЦЙХвЧђХФКЭУПИіЦЙХвЧђЕФЕЅМлЮЊЖрЩйдЊ.
ЃЈ2ЃЉШєУПАрХф4ИБЦЙХвЧђХФКЭ40ИіЦЙХвЧђЃЌдђМзЩЬЕъЕФЗбгУЮЊ дЊЃЌввЩЬЕъЕФЗбгУЮЊ дЊ.
ЃЈ3ЃЉУПАрХф4ИБЦЙХвЧђХФКЭmЃЈmЃО100ЃЉИіЦЙХвЧђдђМзЩЬЕъЕФЗбгУЮЊ дЊЃЌввЩЬЕъЕФЗбгУЮЊ дЊ.
ЃЈ4ЃЉШєИУаЃжЛдквЛМвЩЬЕъЙКТђЃЌФуШЯЮЊдкФФМвГЌЪаЙКТђИќЛЎЫуЃП
ЁОД№АИЁПЃЈ1ЃЉУПИБЦЙХвЧђХФЕЅМлЮЊ50дЊЃЌУПИіЦЙХвЧђЕФЕЅМлЮЊ1дЊЃЛЃЈ2ЃЉ4000дЊ ЃЌ 4320дЊ ЃЛЃЈ3ЃЉ3200+20mЃЌ3600+18mЃЛЃЈ4ЃЉШєМзЩЬЕъЛЈЧЎЩйЃЌдђ3200+20mЃМ3600+18mЃЛНтЕУmЃМ200ЃЛШєввЩЬЕъЛЈЗбЩйЃЌдђ3200+20mЃО3600+18mЃЌНтЕУmЃО200ЃЛШєМзЩЬЕъКЭввЩЬЕъвЛбљЖрЪБЃЌдђ3200+20m=3600+18mЃЌНтЕУm=200ЃЛзлЩЯЫљЪі100ЃМmЃМ200ЪБМзЩЬЕъгХЛнmЃО200ЪБввЩЬЕъгХЛнm=200ЪБСНМвЩЬЕъвЛбљ
ЁОНтЮіЁП
ЃЈ1ЃЉЩшУПИБЦЙХвЧђХФЕЅМлЮЊxдЊЃЌУПИіЦЙХвЧђЕФЕЅМлЮЊyдЊ. ИљОнЬтвтСаГіЖўдЊвЛДЮЗНГЬзщЃЌНтД№МДПЩЃЛ
ЃЈ2ЃЉРћгУЃЈ1ЃЉжаЧѓЕУЕФМлИёМДПЩНтД№ЃЛ
ЃЈ3ЃЉЗжБ№гУКЌmЕФДњЪ§ЪНБэЪОдкМзЁЂввСНМвЩЬЕъЙКТђЫљЛЈЕФЗбгУМДПЩЃЛ
ЃЈ4ЃЉРћгУЃЈ3ЃЉЧѓЕУЕФДњЪ§ЪНЃЌНјааЗжРрЬжТлМДПЩ.
НтЃКЃЈ1ЃЉЩшУПИБЦЙХвЧђХФЕЅМлЮЊxдЊЃЌУПИіЦЙХвЧђЕФЕЅМлЮЊyдЊ.
гЩЬтвтПЩжЊ![]()
НтЕУ![]()
Д№ЃКУПИБЦЙХвЧђХФЕЅМлЮЊ50дЊЃЌУПИіЦЙХвЧђЕФЕЅМлЮЊ1дЊ.
ЃЈ2ЃЉМзЩЬЕъЃК![]() ЃЈдЊЃЉЃЛ
ЃЈдЊЃЉЃЛ
ввЩЬЕъЃК![]() ЃЈдЊЃЉ
ЃЈдЊЃЉ
ЙЪД№АИЮЊЃК4000дЊЃЛ4320дЊЃЛ
ЃЈ3ЃЉдкМзЩЬЕъЙКТђЕФЗбгУЮЊЃК![]()
дкввЩЬЕъЙКТђЕФЗбгУЮЊЃК![]()
ЃЈ4ЃЉШєМзЩЬЕъЛЈЧЎЩйЃЌдђ3200+20mЃМ3600+18m
НтЕУmЃМ200
ШєввЩЬЕъЛЈЗбЩйЃЌдђ3200+20mЃО3600+18mЃЌ
НтЕУmЃО200ЃЌ
ШєМзЩЬЕъКЭввЩЬЕъвЛбљЖрЪБЃЌдђ3200+20m=3600+18mЃЌ
НтЕУm=200
злЩЯЫљЪі100ЃМmЃМ200ЪБМзЩЬЕъгХЛн
mЃО200ЪБввЩЬЕъгХЛн
m=200ЪБСНМвЩЬЕъвЛбљ.


 ЛЅЖЏПЮЬУЯЕСаД№АИ
ЛЅЖЏПЮЬУЯЕСаД№АИ МЄЛюЫМЮЌжЧФмбЕСЗПЮЪБЕМбЇСЗЯЕСаД№АИ
МЄЛюЫМЮЌжЧФмбЕСЗПЮЪБЕМбЇСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
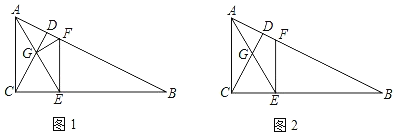
ЁОЬтФПЁПШчЭМ1ЃЌдкRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌCDЁЭABгкDЃЌEЮЊЯпЖЮBCЩЯвЛЕуЃЌAEНЛCDгкGЃЌЧвGCЃНGEЃЌEFЁЭBCНЛABгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКAE2ЃНAFABЃЛ
ЃЈ2ЃЉСЌFGЃЌШєBEЃН2CEЃЌЧѓtanЁЯAFGЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЕБtanBЃНЁЁ ЁЁЪБЃЌCEЃНFEЃЈЧыжБНгаДГіНсЙћЃЌВЛашвЊНтД№Й§ГЬЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§жсЩЯгаСНЕу![]() ЃЌ
ЃЌ![]() ЖдгІЕФЪ§ЗжБ№ЮЊ
ЖдгІЕФЪ§ЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊЪ§жсЩЯвЛЖЏЕуЃЌЖдгІЕуЕФЪ§ЮЊ
ЮЊЪ§жсЩЯвЛЖЏЕуЃЌЖдгІЕуЕФЪ§ЮЊ![]() .
.
ЃЈ1ЃЉШєЕу![]() ЕНЕу
ЕНЕу![]() ЃЌЕу
ЃЌЕу![]() ЕФОрРыЯрЕШЃЌдђЕу
ЕФОрРыЯрЕШЃЌдђЕу![]() ЖдгІЕФЪ§ЮЊ________.
ЖдгІЕФЪ§ЮЊ________.
ЃЈ2ЃЉЪ§жсЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕу
ЃЌЪЙЕу![]() ЕНЕу
ЕНЕу![]() ЁЂЕу
ЁЂЕу![]() ЕФОрРыжЎКЭЮЊ8ЃПШєДцдкЃЌЧыЧѓГі
ЕФОрРыжЎКЭЮЊ8ЃПШєДцдкЃЌЧыЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЃЈ3ЃЉЕБЕу![]() вдУПУы
вдУПУы![]() ЕФЕЅЮЛГЄЖШЕФЫйЖШДг
ЕФЕЅЮЛГЄЖШЕФЫйЖШДг![]() ЃЈдЕуЃЉЯђзѓдЫЖЏЃЌЭЌЪБЕу
ЃЈдЕуЃЉЯђзѓдЫЖЏЃЌЭЌЪБЕу![]() вдУПУы
вдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШЯђзѓдЫЖЏЃЌЕу
ИіЕЅЮЛГЄЖШЕФЫйЖШЯђзѓдЫЖЏЃЌЕу![]() вдУПУы
вдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШЯђзѓдЫЖЏЃЌЮЪЫќУЧЭЌЪБГіЗЂЃЌМИУыКѓЕу
ИіЕЅЮЛГЄЖШЕФЫйЖШЯђзѓдЫЖЏЃЌЮЪЫќУЧЭЌЪБГіЗЂЃЌМИУыКѓЕу![]() ЕНЕу
ЕНЕу![]() ЁЂЕу
ЁЂЕу![]() ЕФОрРыЯрЕШЃП
ЕФОрРыЯрЕШЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭъГЩЯТУцЕФжЄУїЃЎШчЭМЃЌвбжЊABЁЮCDЃЌЁЯB=ЁЯCЃЌ
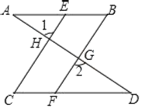
ЧѓжЄЃКЁЯ1=ЁЯ2ЃЎ
жЄУїЃКЁпABЁЮCDЃЈвбжЊЃЉ
ЁрЁЯB=ЁЁ ЁЁЃЈЁЁ ЁЁЃЉЃЎ
ЁпЁЯB=ЁЯCЃЈвбжЊЃЉ
ЁрЁЯBFD=ЁЯCЃЈЕШСПДњЛЛЃЉ
ЁрECЁЮЁЁ ЁЁЃЈЁЁ ЁЁЃЉ
ЁрЁЯ2=ЁЁ ЁЁЃЈСНжБЯпЦНааЃЌЭЌЮЛНЧЯрЕШЃЉ
ЁпЁЯ1=ЁЁ ЁЁЃЈЁЁ ЁЁЃЉ
ЁрЁЯ1=ЁЯ2ЃЈЕШСПДњЛЛЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌ0ЮЊзјБъдЕуЃЌЕуAЕФзјБъЮЊЃЈЃ4ЃЌ0ЃЉЃЌжБЯпBCОЙ§ЕуBЃЈЃ4ЃЌ3ЃЉЃЌCЃЈ0ЃЌ3ЃЉЃЌНЋЫФБпаЮOABCШЦЕуOАДЫГЪБеыЗНЯђа§зЊІСЖШЃЈ0ЃМІСЁмl80ЁуЃЉЕУЕНЫФБпаЮOAЁфBЁфCЁфЃЌДЫЪБжБЯпOAЁфЁЂжБЯпBЁфCЁфЃЌЗжБ№гыжБЯпBCЯрНЛгкPЃЌQЃЎдкЫФБпаЮOABCа§зЊЙ§ГЬжаЃЌШєBP=![]() BQ дђЕуPЕФзјБъЮЊ__________ЃЎ
BQ дђЕуPЕФзјБъЮЊ__________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃЩшМЦСЫШчЭМЫљЪОЕФЕёЫмЃЌШЁУћЁАНзЬнЁБЃЌ ЯждкЙЄГЇЪІИЕДђЫугУгЭЦсХчЫЂЫљгаБЉТЖУцЃЌОВтСПЃЌвбжЊУПИіаЁСЂЗНЬхЕФРтГЄЮЊ0.5Уз.

ЃЈ1ЃЉЧыФуЛГіДгЫќЕФе§УцЁЂзѓУцЁЂЩЯУцШ§ИіВЛЭЌЗНЯђПДЕНЕФЦНУцЭМаЮ.
ЃЈ2ЃЉЧыФуАяжњЙЄШЫЪІИЕМЦЫувЛЯТЃЌашвЊХчЫЂгЭЦсЕФзмУцЛ§ЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉЯШЛЏМђЃЌдйЧѓжЕЃКЃЈ3xЉ6ЃЉЃЈx2Љ![]() ЃЉЉ6xЃЈ
ЃЉЉ6xЃЈ![]() x2ЉxЉ6ЃЉЃЌЦфжаxЃНЉ
x2ЉxЉ6ЃЉЃЌЦфжаxЃНЉ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉвбжЊy2Љ5y+3ЃН0ЃЌЧѓ2ЃЈyЉ1ЃЉЃЈ2yЉ1ЃЉЉ2ЃЈy+1ЃЉ2+7ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯB=90ЁуЃЌAC=60cmЃЌЁЯA=60ЁуЃЌЕуDДгЕуCГіЗЂбиCAЗНЯђвд4cm/УыЕФЫйЖШЯђЕуAдШЫйдЫЖЏЃЌЭЌЪБЕуEДгЕуAГіЗЂбиABЗНЯђвд2cm/УыЕФЫйЖШЯђЕуBдШЫйдЫЖЏЃЌЕБЦфжавЛИіЕуЕНДяжеЕуЪБЃЌСэвЛИіЕувВЫцжЎЭЃжЙдЫЖЏЃЎЩшЕуDЁЂEдЫЖЏЕФЪБМфЪЧtУыЃЈ0ЃМtЁм15ЃЉЃЎЙ§ЕуDзїDFЁЭBCгкЕуFЃЌСЌНгDEЃЌEFЃЎ

ЃЈ1ЃЉЧѓжЄЃКAE=DFЃЛ
ЃЈ2ЃЉЫФБпаЮAEFDФмЙЛГЩЮЊСтаЮТ№ЃПШчЙћФмЃЌЧѓГіЯргІЕФtжЕЃЌШчЙћВЛФмЃЌЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЕБtЮЊКЮжЕЪБЃЌЁїDEFЮЊжБНЧШ§НЧаЮЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАбЯТСаИїЪ§ЗжБ№ЬюШыЯргІЕФМЏКЯРяЃК0ЃЌЃ3.14ЃЌЃ(Ѓ10)ЃЌ![]() ЃЌЃ4
ЃЌЃ4![]() ЃЌ15%ЃЌ
ЃЌ15%ЃЌ![]() ЃЌ0.3ЃЌ
ЃЌ0.3ЃЌ![]() ЃЌ10.01001000100001Ё
ЃЌ10.01001000100001Ё
ЗЧИКећЪ§МЏКЯЃК{ Ё}
е§ЗжЪ§МЏКЯЃК{ Ё}
ЮоРэЪ§МЏКЯЃК{ Ё}
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com