【题目】完成下面的证明．如图，已知AB∥CD，∠B=∠C，
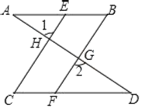
求证：∠1=∠2．
证明：∵AB∥CD（已知）
∴∠B= （ ）．
∵∠B=∠C（已知）
∴∠BFD=∠C（等量代换）
∴EC∥ （ ）
∴∠2= （两直线平行，同位角相等）
∵∠1= （ ）
∴∠1=∠2（等量代换）．
科目：初中数学 来源： 题型：
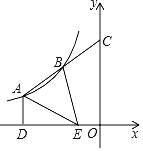
【题目】如图，△ABE中，点A、B是反比例函数y＝
（k≠0）图象上的两点，点E在x轴上，延长线段AB交y轴于点C，点B恰为线段AC中点，过点A作AD⊥x轴于点D．若S△ABE＝
，DE＝2OE，则k的值为（ ）
A.6B.﹣6C.9D.﹣9
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料：大数学家高斯在上学读书时曾经研究过这样一个问题：1+2+3+…+100=？经过研究，这个问题的一般性结论是1+2+3+…+n=
n（n+1），其中n是正整数．现在我们来研究一个类似的问题：1×2+2×3+…n（n+1）=？
观察下面三个特殊的等式：
1×2=
（1×2×3﹣0×1×2）
2×3=
（2×3×4﹣1×2×3）
3×4=
（3×4×5﹣2×3×4）
将这三个等式的两边相加，可以得到1×2+2×3+3×4=
×3×4×5=20，
读完这段材料，请你思考后回答：
（1）1×2+2×3+…+10×11=________________；
（2）1×2+2×3+3×4+…+n×（n+1）=_________________________；
（3）1×2×3+2×3×4+…+n（n+1）（n+2）=______________________________．
（只需写出结果，不必写中间的过程）
查看答案和解析>>
科目：初中数学 来源： 题型：
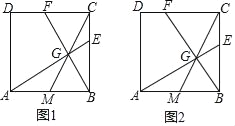
【题目】已知正方形ABCD，点M为边AB的中点．
（1）如图1，点G为线段CM上的一点，且∠AGB=90°，延长AG、BG分别与边BC、CD交于点E、F．
①求证：BE=CF；
②求证：BE2=BCCE．
（2）如图2，在边BC上取一点E，满足BE2=BCCE，连接AE交CM于点G，连接BG并延长交CD于点F，求tan∠CBF的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AD⊥BC于D，BD=AD，DG=DC，E，F分别是BG，AC的中点．
（1）求证：DE=DF，DE⊥DF；
（2）连接EF，若AC=10，求EF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了丰富同学们的课外活动，决定给全校20个班每班配4副乒乓球拍和若干乒乓球，两家体育用品商店对同一款乒乓球拍和乒乓球推出让利活动，甲商店买一副乒乓球拍送10个乒乓球，乙商店所有商品均打九折（按标价的90％）销售，已知2副乒乓球拍和10个乒乓球110元，3副乒乓球拍和20个乒乓球170元。
请解答下列问题：
（1）求每副乒乓球拍和每个乒乓球的单价为多少元.
（2）若每班配4副乒乓球拍和40个乒乓球，则甲商店的费用为 元，乙商店的费用为 元.
（3）每班配4副乒乓球拍和m（m＞100）个乒乓球则甲商店的费用为 元，乙商店的费用为 元.
（4）若该校只在一家商店购买，你认为在哪家超市购买更划算？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC三个顶点的坐标分别为A（2，4），B（1，1），C（4，3）．
(1)请画出△ABC关于x轴对称的△A1B1C1，并写出点A1的坐标；
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2；
(3)求出(2)中C点旋转到C2点所经过的路径长（结果保留根号和π）；
(4)求出(2)△A2BC2的面积是多少．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
