
【题目】已知正方形ABCD,点M为边AB的中点.
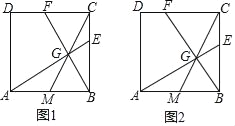
(1)如图1,点G为线段CM上的一点,且∠AGB=90°,延长AG、BG分别与边BC、CD交于点E、F.
①求证:BE=CF;
②求证:BE2=BCCE.
(2)如图2,在边BC上取一点E,满足BE2=BCCE,连接AE交CM于点G,连接BG并延长交CD于点F,求tan∠CBF的值.
【答案】(1)①证明见解析;②证明见解析;(2)![]() .
.
【解析】【试题分析】
(1)①在正方形ABCD中,AB=BC,∠ABC=∠BCF=90°,
因为∠ABG+∠CBF=90°,∠ABG+∠BAG=90°,根据同角的余角相等,得∠BAG=∠CBF,利用ASA判定定理得△ABE≌△BCF,根据全等三角形的对应边相等得:BE=CF.
②∠AGB=90°,点M为AB的中点,直角三角形斜边上的中线等于斜边的一半,得,MG=MA=MB,根据等边对等角得∠GAM=∠AGM.
因为∠CGE=∠AGM,等量代换得∠GAM=∠CGE.
由①可知∠GAM=∠CBG,则∠CGE=∠CBG.
又因为∠ECG=∠GCB,根据两角对应相等,两三角形相似得:△CGE∽△CBG,根据相似三角形对应边成比例得:![]() ,即CG2=BC·CE.∵MG=MB,∴∠MGB=∠MBG.
,即CG2=BC·CE.∵MG=MB,∴∠MGB=∠MBG.
在正方形ABCD中,因为AB∥CD,根据平行线的性质得∠MBG=∠CFG.
又因为∠CGF=∠MGB,等量代换得∠CFG=∠CGF,根据等边对等角得CF=CG.
由①可知BE=CF,即BE=CG,故BE2=BC·CE.
(2)延长AE,DC交于点N.在正方形ABCD中, AB=BC,AB∥CD,∴△CEN∽△BEA,根据相似三角形的对应边成比例得![]() ,即BE·CN=AB·CE.因为AB=BC,
,即BE·CN=AB·CE.因为AB=BC,
则BE2=BC·CE,得CN=BE.由于AB∥DN,得△CGN∽△MGA,△CGF∽△MGB,
则 ![]() ,
,![]() ,∴
,∴![]() . 又因为点M为AB的中点,得MA=MB,
. 又因为点M为AB的中点,得MA=MB,
则CN=CF=BE.
设正方形的边长为a,BE=x,则CE=BC-BE=a-x.由BE2=BC·CE列方程得:x2=a·(a-x),解得x1=![]() a,x2=
a,x2=![]() a(舍去),
a(舍去),![]() =
=![]() ,即tan∠CBF=
,即tan∠CBF=![]() =
=![]() =
=![]() .
.
【试题解析】
(1)①∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠BCF=90°,∴∠ABG+∠CBF=90°.∵∠AGB=90°,∴∠ABG+∠BAG=90°,∴∠BAG=∠CBF,∴△ABE≌△BCF,∴BE=CF.
②∵∠AGB=90°,点M为AB的中点,∴MG=MA=MB,∴∠GAM=∠AGM.
∵∠CGE=∠AGM,∴∠GAM=∠CGE.
由①可知∠GAM=∠CBG,∴∠CGE=∠CBG.
又∵∠ECG=∠GCB,∴△CGE∽△CBG,∴![]() ,
,
即CG2=BC·CE.∵MG=MB,∴∠MGB=∠MBG.
∵四边形ABCD是正方形,∴AB∥CD,∴∠MBG=∠CFG.
又∵∠CGF=∠MGB,∴∠CFG=∠CGF,∴CF=CG.
由①可知BE=CF,∴BE=CG,∴BE2=BC·CE.
(2)延长AE,DC交于点N.∵四边形ABCD是正方形,∴AB=BC,AB∥CD,∴△CEN∽△BEA,∴![]() ,即BE·CN=AB·CE.∵AB=BC,BE2=BC·CE,∴CN=BE.∵AB∥DN,∴△CGN∽△MGA,△CGF∽△MGB,∴
,即BE·CN=AB·CE.∵AB=BC,BE2=BC·CE,∴CN=BE.∵AB∥DN,∴△CGN∽△MGA,△CGF∽△MGB,∴ ![]() ,
,![]() ,∴
,∴![]() . ∵点M为AB的中点,∴MA=MB,∴CN=CF,∴CF=BE.
. ∵点M为AB的中点,∴MA=MB,∴CN=CF,∴CF=BE.
设正方形的边长为a,BE=x,则CE=BC-BE=a-x.由BE2=BC·CE可得x2=a·(a-x),解得x1=![]() a,x2=
a,x2=![]() a(舍去),∴
a(舍去),∴![]() =
=![]() ,∴tan∠CBF=
,∴tan∠CBF=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】恒昌路是一条东西走向的马路,有市场、医院、车站、学校四家公共场所。已知市场在医院东200米,车站在市场东150米,医院在学校东450米。若将马路近似的看成一条直线,以医院为原点,向东方向为正方向,用1个单位长度表示100米,
(1)在数轴上表示出四家公共场所的位置;
![]()
(2)列式计算学校与车站之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017湖北省十堰市,第10题,3分)如图,直线![]() 分别交x轴,y轴于A,B,M是反比例函数
分别交x轴,y轴于A,B,M是反比例函数![]() (x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,ACBD=
(x>0)的图象上位于直线上方的一点,MC∥x轴交AB于C,MD⊥MC交AB于D,ACBD=![]() ,则k的值为( )
,则k的值为( )
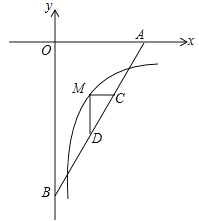
A. ﹣3 B. ﹣4 C. ﹣5 D. ﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有两点![]() ,
,![]() 对应的数分别为
对应的数分别为![]() ,
,![]() ,点
,点![]() 为数轴上一动点,对应点的数为
为数轴上一动点,对应点的数为![]() .
.
(1)若点![]() 到点
到点![]() ,点
,点![]() 的距离相等,则点
的距离相等,则点![]() 对应的数为________.
对应的数为________.
(2)数轴上是否存在点![]() ,使点
,使点![]() 到点
到点![]() 、点
、点![]() 的距离之和为8?若存在,请求出
的距离之和为8?若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3)当点![]() 以每秒
以每秒![]() 的单位长度的速度从
的单位长度的速度从![]() (原点)向左运动,同时点
(原点)向左运动,同时点![]() 以每秒
以每秒![]() 个单位长度的速度向左运动,点
个单位长度的速度向左运动,点![]() 以每秒
以每秒![]() 个单位长度的速度向左运动,问它们同时出发,几秒后点
个单位长度的速度向左运动,问它们同时出发,几秒后点![]() 到点
到点![]() 、点
、点![]() 的距离相等?
的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图中的小方格都是边长为1的正方形, △ABC与△A′ B′ C′是关于点0为位似中心的位似图形,它们的顶点都在小正方形的顶点上.

(1)画出位似中心点0;
(2)求出△ABC与△A′B′C′的位似比;
(3)以点0为位似中心,再画一个△A1B1C1,使它与△ABC的位似比等于1.5.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明.如图,已知AB∥CD,∠B=∠C,
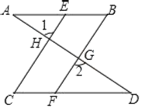
求证:∠1=∠2.
证明:∵AB∥CD(已知)
∴∠B= ( ).
∵∠B=∠C(已知)
∴∠BFD=∠C(等量代换)
∴EC∥ ( )
∴∠2= (两直线平行,同位角相等)
∵∠1= ( )
∴∠1=∠2(等量代换).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校设计了如图所示的雕塑,取名“阶梯”, 现在工厂师傅打算用油漆喷刷所有暴露面,经测量,已知每个小立方体的棱长为0.5米.

(1)请你画出从它的正面、左面、上面三个不同方向看到的平面图形.
(2)请你帮助工人师傅计算一下,需要喷刷油漆的总面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意有理数a,b,定义运算:a⊙b=a(a+b)﹣1,等式右边是通常的加法、减法、乘法运算,例如,2⊙5=2×(2+5)﹣1=13;(﹣3)⊙(﹣5)=﹣3×(﹣3﹣5)﹣1=23.
(1)求(﹣2)⊙3![]() 的值;
的值;
(2)对于任意有理数m,n,请你重新定义一种运算“⊕”,使得5⊕3=20,写出你定义的运算:m⊕n= (用含m,n的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com