
ЁОЬтФПЁПвбжЊЪ§жсЩЯгаСНЕу![]() ЃЌ
ЃЌ![]() ЖдгІЕФЪ§ЗжБ№ЮЊ
ЖдгІЕФЪ§ЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊЪ§жсЩЯвЛЖЏЕуЃЌЖдгІЕуЕФЪ§ЮЊ
ЮЊЪ§жсЩЯвЛЖЏЕуЃЌЖдгІЕуЕФЪ§ЮЊ![]() .
.
ЃЈ1ЃЉШєЕу![]() ЕНЕу
ЕНЕу![]() ЃЌЕу
ЃЌЕу![]() ЕФОрРыЯрЕШЃЌдђЕу
ЕФОрРыЯрЕШЃЌдђЕу![]() ЖдгІЕФЪ§ЮЊ________.
ЖдгІЕФЪ§ЮЊ________.
ЃЈ2ЃЉЪ§жсЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕу
ЃЌЪЙЕу![]() ЕНЕу
ЕНЕу![]() ЁЂЕу
ЁЂЕу![]() ЕФОрРыжЎКЭЮЊ8ЃПШєДцдкЃЌЧыЧѓГі
ЕФОрРыжЎКЭЮЊ8ЃПШєДцдкЃЌЧыЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩ.
ЃЈ3ЃЉЕБЕу![]() вдУПУы
вдУПУы![]() ЕФЕЅЮЛГЄЖШЕФЫйЖШДг
ЕФЕЅЮЛГЄЖШЕФЫйЖШДг![]() ЃЈдЕуЃЉЯђзѓдЫЖЏЃЌЭЌЪБЕу
ЃЈдЕуЃЉЯђзѓдЫЖЏЃЌЭЌЪБЕу![]() вдУПУы
вдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШЯђзѓдЫЖЏЃЌЕу
ИіЕЅЮЛГЄЖШЕФЫйЖШЯђзѓдЫЖЏЃЌЕу![]() вдУПУы
вдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШЯђзѓдЫЖЏЃЌЮЪЫќУЧЭЌЪБГіЗЂЃЌМИУыКѓЕу
ИіЕЅЮЛГЄЖШЕФЫйЖШЯђзѓдЫЖЏЃЌЮЪЫќУЧЭЌЪБГіЗЂЃЌМИУыКѓЕу![]() ЕНЕу
ЕНЕу![]() ЁЂЕу
ЁЂЕу![]() ЕФОрРыЯрЕШЃП
ЕФОрРыЯрЕШЃП
ЁОД№АИЁПЃЈ1ЃЉ1ЃЛЃЈ2ЃЉ-3Лђ5ЃЛЃЈ3ЃЉ![]() УыЛђ
УыЛђ![]() Уы
Уы
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтСаЗНГЬМДПЩЕУЕННсТлЃЛ
ЃЈ2ЃЉРћгУЕБAдкMзѓВрЪБЃЌЕБAдкNгвВрЪБЃЌЗжБ№ЕУГіМДПЩЃЛ
ЃЈ3ЃЉРћгУЕБAЕудкMЁЂNжЎМфЪБЃЌДЫЪБNЕНAЕуОрРыЕШгкMЕуЕНAЕуОрРыЃЌвдМАЕБAЕудкMЁЂNгвВрЪБЃЌДЫЪБMЁЂNжиКЯЃЌЧѓГіМДПЩЃЎ
НтЃКЃЈ1ЃЉИљОнЬтвтЕУЃЌa-ЃЈ-2ЃЉ=4-aЃЌ
Ёрa=1ЃЌ
ЙЪД№АИЮЊЃК1ЃЛ
ЃЈ2ЃЉДцдкЃЌ
ЁпЕуAЕНЕуMЁЂЕуNЕФОрРыжЎКЭЮЊ8ЃЌ
Ёр|a+2|+|a-4|=8ЃЌ
ЕБaЁм-2ЪБЃЌдЗНГЬПЩЛЏЮЊЃК-a-2+4-a=8ЃЌНтЕУa=-3ЃЛ
ЕБ-2ЃМaЃМ4ЪБЃЌдЗНГЬПЩЛЏЮЊЃКa+2+4-a=8ЃЌдђ4=5ЃЈЩсЃЉ
ЕБaЁн4ЪБЃЌдЗНГЬПЩЛЏЮЊЃКa+2+a-4=8ЃЌНтЕУa=5ЃЛ
злЩЯЃКЕуAЖдгІЕФЪ§ЮЊ-3Лђ5ЪБЃЌЫќЕНЕуMЁЂЕуNЕФОрРыжЎКЭЮЊ8ЃЛ
ЃЈ3ЃЉЩшЭЌЪБГіЗЂxУыКѓЕуAЕНЕуMЁЂЕуNЕФОрРыЯрЕШЃЎ
ЂйЕуAдкЕуMгыЕуNжЎМфЃЌ
ИљОнЬтвтЃЌЕУ
10x+2-2x=2x+4-40x,
НтЕУx= ![]() ЃЛ
ЃЛ
ЂкЕуNзЗЩЯЕуMЪБЃЌИљОнЬтвтЕУ
40x-10x=6ЃЌ
НтЕУx=![]() ЃЌ
ЃЌ
Д№ЃКЭЌЪБГіЗЂ![]() УыЛђ
УыЛђ![]() УыКѓЕуAЕНЕуMЁЂЕуNЕФОрРыЯрЕШЃЎ
УыКѓЕуAЕНЕуMЁЂЕуNЕФОрРыЯрЕШЃЎ


 вЛПЮвЛСЗПЮЪБДяБъЯЕСаД№АИ
вЛПЮвЛСЗПЮЪБДяБъЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙХЯЃРАжјУћЕФБЯДяИчРЫЙбЇХЩАб1ЃЌ3ЃЌ6ЃЌ10ЁетбљЕФЪ§ГЦЮЊЁАШ§НЧаЮЪ§ЁБЃЌЖјАб1ЃЌ4ЃЌ9ЃЌ16ЁетбљЕФЪ§ГЦЮЊЁАе§ЗНаЮЪ§ЁБЃЎДгЭМжаПЩвдЗЂЯжЃЌШЮКЮвЛИіДѓгк1ЕФЁАе§ЗНаЮЪ§ЁБЖМПЩвдПДзїСНИіЯрСкЁАШ§НЧаЮЪ§ЁБжЎКЭЃЎЯТСаЕШЪНжаЃЌЗћКЯетвЛЙцТЩЕФЪЧЃЈЁЁЁЁЃЉ

A. 36ЃН15ЃЋ21 B. 25ЃН9ЃЋ16 C. 13ЃН3ЃЋ10 D. 49ЃН18ЃЋ31
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(1)ШчЭМЃЌдке§ЗНаЮABCDжаЃЌEЪЧABЩЯвЛЕуЃЌGЪЧADЩЯвЛЕуЃЌЁЯECG=45ЁуЃЌФЧУДEGгыЭМжаСНЬѕЯпЖЮЕФКЭЯрЕШЃПжЄУїФуЕФНсТл.
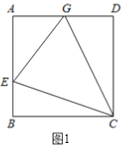
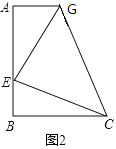
(2)ЧыгУ(1)жаЫљЛ§РлЕФОбщКЭжЊЪЖЭъГЩДЫЬтЃЌШчЭМЃЌдкЫФБпаЮABCGжаЃЌAG//BC(BC>AG)ЃЌЁЯB=90ЁуЃЌAB=BC=12ЃЌEЪЧABЩЯвЛЕуЃЌЧвЁЯECG=45ЁуЃЌBE=4ЃЌЧѓEGЕФГЄ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСВФСЯЃКДѓЪ§бЇМвИпЫЙдкЩЯбЇЖСЪщЪБдјОбаОПЙ§етбљвЛИіЮЪЬтЃК1+2+3+Ё+100=ЃПОЙ§баОПЃЌетИіЮЪЬтЕФвЛАуадНсТлЪЧ1+2+3+Ё+n=![]() nЃЈn+1ЃЉЃЌЦфжаnЪЧе§ећЪ§ЃЎЯждкЮвУЧРДбаОПвЛИіРрЫЦЕФЮЪЬтЃК1ЁС2+2ЁС3+ЁnЃЈn+1ЃЉ=ЃП
nЃЈn+1ЃЉЃЌЦфжаnЪЧе§ећЪ§ЃЎЯждкЮвУЧРДбаОПвЛИіРрЫЦЕФЮЪЬтЃК1ЁС2+2ЁС3+ЁnЃЈn+1ЃЉ=ЃП
ЙлВьЯТУцШ§ИіЬиЪтЕФЕШЪНЃК
1ЁС2=![]() ЃЈ1ЁС2ЁС3Љ0ЁС1ЁС2ЃЉ
ЃЈ1ЁС2ЁС3Љ0ЁС1ЁС2ЃЉ
2ЁС3=![]() ЃЈ2ЁС3ЁС4Љ1ЁС2ЁС3ЃЉ
ЃЈ2ЁС3ЁС4Љ1ЁС2ЁС3ЃЉ
3ЁС4=![]() ЃЈ3ЁС4ЁС5Љ2ЁС3ЁС4ЃЉ
ЃЈ3ЁС4ЁС5Љ2ЁС3ЁС4ЃЉ
НЋетШ§ИіЕШЪНЕФСНБпЯрМгЃЌПЩвдЕУЕН1ЁС2+2ЁС3+3ЁС4=![]() ЁС3ЁС4ЁС5=20ЃЌ
ЁС3ЁС4ЁС5=20ЃЌ
ЖСЭъетЖЮВФСЯЃЌЧыФуЫМПМКѓЛиД№ЃК
ЃЈ1ЃЉ1ЁС2+2ЁС3+Ё+10ЁС11=________________ЃЛ
ЃЈ2ЃЉ1ЁС2+2ЁС3+3ЁС4+Ё+nЁСЃЈn+1ЃЉ=_________________________ЃЛ
ЃЈ3ЃЉ1ЁС2ЁС3+2ЁС3ЁС4+Ё+nЃЈn+1ЃЉЃЈn+2ЃЉ=______________________________ЃЎ
ЃЈжЛашаДГіНсЙћЃЌВЛБиаДжаМфЕФЙ§ГЬЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСтаЮOABCЕФвЛБпOAдкxжсЕФИКАыжсЩЯЃЌOЪЧзјБъдЕуЃЌtanЁЯAOC=![]() ЃЌЗДБШР§КЏЪ§y=
ЃЌЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓОЙ§ЕуCЃЌгыABНЛгкЕуDЃЌШєЁїCODЕФУцЛ§ЮЊ20ЃЌдђkЕФжЕЕШгк_____ЃЎ
ЕФЭМЯѓОЙ§ЕуCЃЌгыABНЛгкЕуDЃЌШєЁїCODЕФУцЛ§ЮЊ20ЃЌдђkЕФжЕЕШгк_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊе§ЗНаЮABCDЃЌЕуMЮЊБпABЕФжаЕуЃЎ
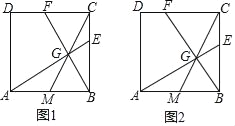
ЃЈ1ЃЉШчЭМ1ЃЌЕуGЮЊЯпЖЮCMЩЯЕФвЛЕуЃЌЧвЁЯAGB=90ЁуЃЌбгГЄAGЁЂBGЗжБ№гыБпBCЁЂCDНЛгкЕуEЁЂFЃЎ
ЂйЧѓжЄЃКBE=CFЃЛ
ЂкЧѓжЄЃКBE2=BCCEЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌдкБпBCЩЯШЁвЛЕуEЃЌТњзуBE2=BCCEЃЌСЌНгAEНЛCMгкЕуGЃЌСЌНгBGВЂбгГЄНЛCDгкЕуFЃЌЧѓtanЁЯCBFЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌADЁЭBCгкDЃЌBD=ADЃЌDG=DCЃЌEЃЌFЗжБ№ЪЧBGЃЌACЕФжаЕуЃЎ
ЃЈ1ЃЉЧѓжЄЃКDE=DFЃЌDEЁЭDFЃЛ
ЃЈ2ЃЉСЌНгEFЃЌШєAC=10ЃЌЧѓEFЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫЗсИЛЭЌбЇУЧЕФПЮЭтЛюЖЏЃЌОіЖЈИјШЋаЃ20ИіАрУПАрХф4ИБЦЙХвЧђХФКЭШєИЩЦЙХвЧђЃЌСНМвЬхг§гУЦЗЩЬЕъЖдЭЌвЛПюЦЙХвЧђХФКЭЦЙХвЧђЭЦГіШУРћЛюЖЏЃЌМзЩЬЕъТђвЛИБЦЙХвЧђХФЫЭ10ИіЦЙХвЧђЃЌввЩЬЕъЫљгаЩЬЦЗОљДђОХелЃЈАДБъМлЕФ90ЃЅЃЉЯњЪлЃЌвбжЊ2ИБЦЙХвЧђХФКЭ10ИіЦЙХвЧђ110дЊЃЌ3ИБЦЙХвЧђХФКЭ20ИіЦЙХвЧђ170дЊЁЃ
ЧыНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓУПИБЦЙХвЧђХФКЭУПИіЦЙХвЧђЕФЕЅМлЮЊЖрЩйдЊ.
ЃЈ2ЃЉШєУПАрХф4ИБЦЙХвЧђХФКЭ40ИіЦЙХвЧђЃЌдђМзЩЬЕъЕФЗбгУЮЊ дЊЃЌввЩЬЕъЕФЗбгУЮЊ дЊ.
ЃЈ3ЃЉУПАрХф4ИБЦЙХвЧђХФКЭmЃЈmЃО100ЃЉИіЦЙХвЧђдђМзЩЬЕъЕФЗбгУЮЊ дЊЃЌввЩЬЕъЕФЗбгУЮЊ дЊ.
ЃЈ4ЃЉШєИУаЃжЛдквЛМвЩЬЕъЙКТђЃЌФуШЯЮЊдкФФМвГЌЪаЙКТђИќЛЎЫуЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТБэЪЧФГЫЎПтвЛжмФкЫЎЮЛИпЕЭЕФБфЛЏЧщПі(гУе§Ъ§МЧЫЎЮЛБШЧАвЛШеЩЯЩ§Ъ§ЃЌгУИКЪ§МЧЯТНЕЪ§)ЃЎФЧУДБОжмаЧЦкМИЫЎЮЛзюЕЭ ЃЈ ЃЉ

A. аЧЦкЖўB. аЧЦкЫФC. аЧЦкСљD. аЧЦкЮх
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com