
【题目】某景区经营一种新上市的纪念品,进价为20元/件.试营销阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.设这种纪念品的销售单价为x(元).
(1)求每天所得的销售利润y(元)与销售单价x(元)之间的函数关系式;
(2)求销售单价为多少元时,该纪念品每天的销售利润最大;
(3)若要求每天销售量不少于10件,且每件文具的利润至少为25元,则该纪念品的最大利润是多少?
【答案】(1)y=﹣10x2+700x﹣10000;(2)销售单价为35元时,该纪念品每天的销售利润最大为2250元;(3)该纪念品的最大利润是1250元.
【解析】
(1)根据利润=(单价-进价)×实际销售量,而实际销售量=原销售量-10![]() 上涨的钱数,列出函数关系式即可;
上涨的钱数,列出函数关系式即可;
(2)根据(1)式列出的函数关系式,运用配方法求最大值;
(3)求出方案中x的取值范围,然后求出方案的最大利润.
(1)y=(x﹣20)[250﹣10(x﹣25)]
=﹣10x2+700x﹣10000
∴每天所得的销售利润y(元)与销售单价x(元)之间的函数关系式:y=﹣10x2+700x﹣10000;
(2)y=﹣10x2+700x﹣10000
=﹣10(x﹣35)2+2250
∴当x=35时销售利润最大为2250元;
(3)∵250﹣10(x﹣25)≥10,x﹣20≥25
∴45≤x≤49
∵y=﹣10(x﹣35)2+2250的对称轴为:x=35且图象开口向下
∴x=45时,y有最大值1250元.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】为活跃联欢晚会的气氛,组织者设计了以下转盘游戏:A、B两个带指针的转盘分别被分成三个面积相等的扇形,转盘A上的数字分别是1,6,8,转盘B上的数字分别是4,5,7(两个转盘除表面数字不同外,其他完全相同).每次选择2名同学分别拨动A、B两个转盘上的指针,使之产生旋转,指针停止后所指数字较大的一方为获胜者,负者则表演一个节目(若箭头恰好停留在分界线上,则重转一次).作为游戏者,你会选择A、B中哪个转盘呢?并请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
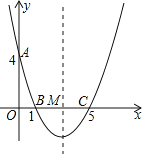
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一点,
上一点,![]() ,连接
,连接![]() .
.
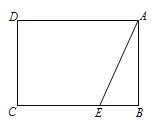
(1)沿![]() 翻折
翻折![]() 使点
使点![]() 落在点
落在点![]() 处,
处,
①连接![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
②连接![]() ,若
,若![]() ,求
,求![]() 的取值范围.
的取值范围.
(2)![]() 绕点
绕点![]() 顺时针旋转得
顺时针旋转得![]() ,点
,点![]() 落在边
落在边![]() 上时旋转停止. 若点
上时旋转停止. 若点![]() 落在矩形对角线
落在矩形对角线![]() 上,且点
上,且点![]() 到
到![]() 的距离小于
的距离小于![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
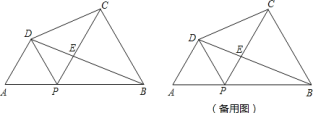
【题目】如图,已知线段![]() ,
,![]() 是线段
是线段![]() 上任意一点(不与点
上任意一点(不与点![]() 、
、![]() 重合),分别以
重合),分别以![]() 、
、![]() 为边,在
为边,在![]() 的同侧作等边
的同侧作等边![]() 和
和![]() ,连接
,连接![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() .
.
![]() 当
当![]() 时,试求
时,试求![]() 的正切值;
的正切值;
![]() 若线段
若线段![]() 是线段
是线段![]() 和
和![]() 的比例中项,试求这时
的比例中项,试求这时![]() 的值;
的值;
![]() 记四边形
记四边形![]() 的面积为
的面积为![]() ,当
,当![]() 在线段
在线段![]() 上运动时,
上运动时,![]() 与
与![]() 是否成正比例,若成正比例,试求出比例系数;若不成正比例,试说明理由.
是否成正比例,若成正比例,试求出比例系数;若不成正比例,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com