
【题目】已知二次函数y=ax2+bx+c图象的对称轴为y轴,且过点(1,2),(2,5).

(1)求二次函数的解析式;
(2)如图,过点E(O,2)的一次函数图象与二次函数的图象交于A,B两点(A点在B点的左侧),过点A,B分别作AC⊥x轴于点C,BD⊥x轴于点D。
①当CD=3时,求该一次函数的解析式;
②分别用S1,S2,S3表示△ACE,△ECD,△EDB的面积,问是否存在实数t,使得![]() =tS1S3,都成立?若存在,求出t的值;若不存在,说明理由。
=tS1S3,都成立?若存在,求出t的值;若不存在,说明理由。
【答案】(1)![]() ;(2)①
;(2)①![]() 或
或![]() ,②存在实数
,②存在实数![]() ,使得
,使得![]() 成立,理由见解析
成立,理由见解析
【解析】
(1)根据对称轴方程、和过点(1,2),(2,5),用待定系数法即可解答.
(2)①设过点![]() 的一次函数的解析式为
的一次函数的解析式为![]() ,则
,则![]() ,解得m=2,即该一次函数的解析式为
,解得m=2,即该一次函数的解析式为![]() . 设
. 设![]() ,
,![]() ,则
,则![]() ,
,![]() .将
.将![]() 代入
代入![]() ,得
,得![]() ,再由
,再由![]() 即可求出解得k
即可求出解得k![]() ,所以一次函数的解析式是
,所以一次函数的解析式是![]() 或
或![]() .
.
②根据三角形面积公式可得![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,即S1S3=-
,即S1S3=-![]() x1y1·
x1y1·![]() x2y2=-
x2y2=-![]() x1 x2(kx1+2)( kx2+2)= -
x1 x2(kx1+2)( kx2+2)= -![]() x1 x2[k2x1x2+2k(x1 +x2)+4]从而求解.
x1 x2[k2x1x2+2k(x1 +x2)+4]从而求解.
(1)依题意,得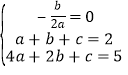 ,解得
,解得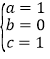 ,
,
∴二次函数的解析式为![]() .
.
(2)设过点![]() 的一次函数的解析式为
的一次函数的解析式为![]() ,
,
则![]() ,
,
∴![]() ,
,
即该一次函数的解析式为![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
将![]() 代入
代入![]() ,得
,得![]() ,
,
即![]() ,
,
解得![]() ,
,
∴![]() ,
,![]() .
.
①依题意,
得![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴该一次函数的解析式是![]() 或
或![]() .
.
②依题意,得![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
![]()
![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
![]()
![]() ,
,
∴![]() ,
,
故存在实数![]() ,使得
,使得![]() 成立.
成立.


科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.

(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
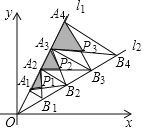
【题目】如图,A1,A2,A3…,An,An+1是直线![]() 上的点,且OA1=A1A2=A2A3=…AnAn+1=2,分别过点A1,A2,A3…,An,An+1作l1的垂线与直线
上的点,且OA1=A1A2=A2A3=…AnAn+1=2,分别过点A1,A2,A3…,An,An+1作l1的垂线与直线![]() 相交于点B1,B2,B3…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3…,AnBn+1,BnAn+1,交点依次为P1,P2,P3…,Pn,设△P1A1A2,△P2A2A3,△P3A3A4,…,△PnAnAn+1的面积分别为S1,S2,S3…,Sn,则Sn=______.(用含有正整数n的式子表示)
相交于点B1,B2,B3…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3…,AnBn+1,BnAn+1,交点依次为P1,P2,P3…,Pn,设△P1A1A2,△P2A2A3,△P3A3A4,…,△PnAnAn+1的面积分别为S1,S2,S3…,Sn,则Sn=______.(用含有正整数n的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,滑动调节式遮阳伞的立柱![]() 垂直于地面
垂直于地面![]() ,
,![]() 为立柱上的滑动调节点,伞体的截面示意图为
为立柱上的滑动调节点,伞体的截面示意图为![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,
,![]() .当点
.当点![]() 位于初始位置
位于初始位置![]() 时,点
时,点![]() 与
与![]() 重合(图2).根据生活经验,当太阳光线与
重合(图2).根据生活经验,当太阳光线与![]() 垂直时,遮阳效果最佳.
垂直时,遮阳效果最佳.
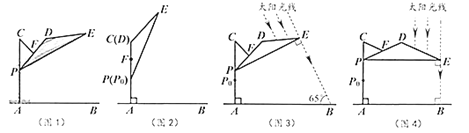
(1)上午10:00时,太阳光线与地面的夹角为![]() (图3),为使遮阳效果最佳,点
(图3),为使遮阳效果最佳,点![]() 需从
需从![]() 上调多少距离?(结果精确到
上调多少距离?(结果精确到![]() )
)
(2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点![]() 在(1)的基础上还需上调多少距离?(结果精确到
在(1)的基础上还需上调多少距离?(结果精确到![]() )
)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
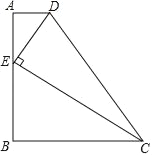
【题目】如图,在四边形ABCD中,AD∥BC,AB⊥BC,点E在AB上,∠DEC=90°.
(1)求证:△ADE∽△BEC.
(2)若AD=1,BC=3,AE=2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
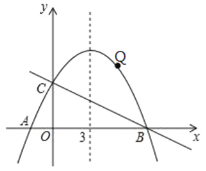
【题目】如图,已知抛物线y=ax+![]() x+4的对称轴是直线x=3,且与轴相交于A、B两点(B点在A点的右侧),与轴交于C点.
x+4的对称轴是直线x=3,且与轴相交于A、B两点(B点在A点的右侧),与轴交于C点.
(1)求出A点的坐标、B点坐标;
(2)求出直线BC的解析式;
(3)点Q是直线BC上方的抛物线上的一动点(不与B、C重合),是否存在点Q,使△QBC的面积最大.若存在,请求出△QBC的最大面积,若不存在,试说明理由;
(4)若E在x轴上,点F在抛物线上,以A、C、E、F为顶点的四边形是平行四边形时,请直接写出点E的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是二次函数y=ax2+bx+c(a≠0)图象的一部分,直线x=﹣1是对称轴,有下列判断:①b﹣2a=0,②4a﹣2b+c<0,③a﹣b+c=﹣9a,④若(﹣3,y1),(![]() ,y2)是抛物线上的两点,则y1<y2.其中正确的是( )
,y2)是抛物线上的两点,则y1<y2.其中正确的是( )
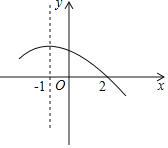
A. ①②③B. ①③C. ①④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴的交点的横坐标分别为-1,3,则下列结论正确的个数有( )①ac<0;②2a+b=0;③4a+2b+c>0;④对于任意x均有ax2+bx≥a+b.
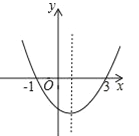
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在长方形ABCD中,AB=12cm,BC=10cm,点P从A出发,沿A→B→C→D的路线运动,到D停止;点Q从D点出发,沿D→C→B→A路线运动,到A点停止.若P、Q两点同时出发,速度分别为每秒lcm、2cm,a秒时P、Q两点同时改变速度,分别变为每秒2cm、![]() cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
cm(P、Q两点速度改变后一直保持此速度,直到停止),如图2是△APD的面积s(cm2)和运动时间x(秒)的图象.
(1)求出a值;
(2)设点P已行的路程为y1(cm),点Q还剩的路程为y2(cm),请分别求出改变速度后,y1、y2和运动时间x(秒)的关系式;
(3)求P、Q两点都在BC边上,x为何值时P、Q两点相距3cm?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com