
【题目】如图1,滑动调节式遮阳伞的立柱![]() 垂直于地面
垂直于地面![]() ,
,![]() 为立柱上的滑动调节点,伞体的截面示意图为
为立柱上的滑动调节点,伞体的截面示意图为![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,
,![]() .当点
.当点![]() 位于初始位置
位于初始位置![]() 时,点
时,点![]() 与
与![]() 重合(图2).根据生活经验,当太阳光线与
重合(图2).根据生活经验,当太阳光线与![]() 垂直时,遮阳效果最佳.
垂直时,遮阳效果最佳.
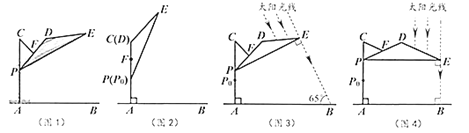
(1)上午10:00时,太阳光线与地面的夹角为![]() (图3),为使遮阳效果最佳,点
(图3),为使遮阳效果最佳,点![]() 需从
需从![]() 上调多少距离?(结果精确到
上调多少距离?(结果精确到![]() )
)
(2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点![]() 在(1)的基础上还需上调多少距离?(结果精确到
在(1)的基础上还需上调多少距离?(结果精确到![]() )
)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
【答案】(1)点![]() 需从
需从![]() 上调
上调![]() ;(2)点
;(2)点![]() 在(1)的基础上还需上调
在(1)的基础上还需上调![]() .
.
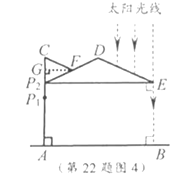
【解析】(1)如图2,当点![]() 位于初始位置
位于初始位置![]() 时,
时,![]() . 10:00时,太阳光线与地面的夹角为
. 10:00时,太阳光线与地面的夹角为![]() ,点
,点![]() 上调至
上调至![]() 处,
处,![]() .
.![]() ,
,![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,即可求出点
,即可求出点![]() 需从
需从![]() 上调的距离.
上调的距离.
(2)中午12:00时,太阳光线与![]() ,地面都垂直,点
,地面都垂直,点![]() 上调至
上调至![]() 处,过点
处,过点![]() 作
作![]() 于点
于点![]() ,
,![]() ,
,![]() ,根据
,根据![]() 即可求解.
即可求解.
【解答】(1)如图2,当点![]() 位于初始位置
位于初始位置![]() 时,
时,![]() .
.
如图3,10:00时,太阳光线与地面的夹角为![]() ,点
,点![]() 上调至
上调至![]() 处,
处,
![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() 为等腰直角三角形,∴
为等腰直角三角形,∴![]() ,
,
∴![]() ,
,
即点![]() 需从
需从![]() 上调
上调![]() .
.
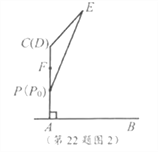

(2)如图4,中午12:00时,太阳光线与![]() ,地面都垂直,点
,地面都垂直,点![]() 上调至
上调至![]() 处,
处,
∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,
,
∴.
∵![]() ,得
,得![]() 为等腰三角形,
为等腰三角形,
∴![]() .
.
过点![]() 作
作![]() 于点
于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即点![]() 在(1)的基础上还需上调
在(1)的基础上还需上调![]() .
.


科目:初中数学 来源: 题型:
【题目】某班为了从甲、乙两同学中选出班长,进行了一次演讲答辩和民主测评,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五位老师作为评委,对演讲答辩情况进行评价,结果如下表:演讲答辩得分表,另全班
五位老师作为评委,对演讲答辩情况进行评价,结果如下表:演讲答辩得分表,另全班![]() 位同学则参与民主测评进行投票,结果如下图:民主测评统计图
位同学则参与民主测评进行投票,结果如下图:民主测评统计图
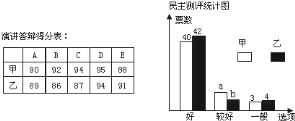
规定:演讲得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评得分![]() “好”票数
“好”票数![]() 分+“较好”票数
分+“较好”票数![]() 分+“一般”票数
分+“一般”票数![]() 分.
分.
![]() 求甲、乙两位选手各自演讲答辩的平均分;
求甲、乙两位选手各自演讲答辩的平均分;
![]() 试求民主测评统计图中
试求民主测评统计图中![]() 、
、![]() 的值是多少?
的值是多少?
![]() 若演讲答辩得分和民主测评得分按
若演讲答辩得分和民主测评得分按![]() 的权重比计算两位选手的综合得分,则应选取哪位选手当班长?
的权重比计算两位选手的综合得分,则应选取哪位选手当班长?
查看答案和解析>>
科目:初中数学 来源: 题型:
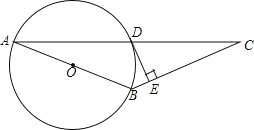
【题目】已知:如图,AB为⊙O的直径,⊙O过AC的中点D,DE⊥BC于点E.
(1)求证:DE为⊙O的切线;
(2)若DE=2,tanC=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点![]() 为二次函数
为二次函数![]() 图象的顶点,直线
图象的顶点,直线![]() 分别交
分别交![]() 轴正半轴,
轴正半轴,![]() 轴于点
轴于点![]() ,
,![]() .
.
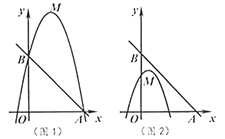
(1)判断顶点![]() 是否在直线
是否在直线![]() 上,并说明理由.
上,并说明理由.
(2)如图1,若二次函数图象也经过点![]() ,
,![]() ,且
,且![]() ,根据图象,写出
,根据图象,写出![]() 的取值范围.
的取值范围.
(3)如图2,点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 内,若点
内,若点![]() ,
,![]() 都在二次函数图象上,试比较
都在二次函数图象上,试比较![]() 与
与![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分.某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是( )
A. 甲 B. 甲与丁 C. 丙 D. 丙与丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为解决楼房之间的挡光问题,某地区规定:两幢楼房间的距离至少为40米,中午12时不能挡光.如图,某旧楼的一楼窗台高1米,要在此楼正南方40米处再建一幢新楼.已知该地区冬天中午12时阳光从正南方照射,并且光线与水平线的夹角最小为30°,在不违反规定的情况下,请问新建楼房最高多少米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点![]() 、点
、点![]() 表示的数分别为
表示的数分别为![]() 、
、![]() ,则
,则![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ,线段
,线段![]() 的中点表示的数为
的中点表示的数为![]() .
.
(问题情境)
如图,数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为8,点
表示的数为8,点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为![]() 秒(
秒(![]() ).
).
(综合运用)
(1)填空:
①![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ________,线段
________,线段![]() 的中点表示的数为__________.
的中点表示的数为__________.
②用含![]() 的代数式表示:
的代数式表示:![]() 秒后,点
秒后,点![]() 表示的数为____________;点
表示的数为____________;点![]() 表示的数为___________.
表示的数为___________.
③当![]() _________时,
_________时,![]() 、
、![]() 两点相遇,相遇点所表示的数为__________.
两点相遇,相遇点所表示的数为__________.
(2)当![]() 为何值时,
为何值时,![]() .
.
(3)若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,点
的中点,点![]() 在运动过程中,线段
在运动过程中,线段![]() 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段
的长度是否发生变化?若变化,请说明理由;若不变,请求出线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个长方形休闲广场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为![]() 米,广场的长为
米,广场的长为![]() 米,宽为
米,宽为![]() 米.
米.
(1)请列式表示花坛的面积和广场空地的面积;
(2)若休闲广场的长为500米,宽为200米,圆形花坛的半径为20米,求广场空地的面积;(计算结果保留![]() ;
;
(3)在(2)的情况下,若![]() 取3.14,求休闲广场的绿化率是多少?
取3.14,求休闲广场的绿化率是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com