
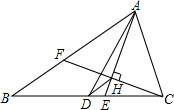
 如图,在△ABC中,AB=5,AC=3,AD、AE分别为△ABC的中线和角平分线,过点C作CH⊥AE于点H,并延长交AB于点F,连结DH,则线段DH的长为1.
如图,在△ABC中,AB=5,AC=3,AD、AE分别为△ABC的中线和角平分线,过点C作CH⊥AE于点H,并延长交AB于点F,连结DH,则线段DH的长为1.  浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
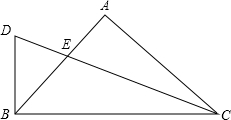 如图,在△ABC中,AB=AC,∠A=90°,CE平分∠ACB,交AB于点E,延长CE作DB⊥BC,垂足为B,则$\frac{CE}{ED}$=$\sqrt{2}$+1.
如图,在△ABC中,AB=AC,∠A=90°,CE平分∠ACB,交AB于点E,延长CE作DB⊥BC,垂足为B,则$\frac{CE}{ED}$=$\sqrt{2}$+1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
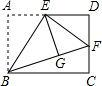 如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=4$\sqrt{6}$,则FD的长为( )
如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=6,BC=4$\sqrt{6}$,则FD的长为( )| A. | 2 | B. | 4 | C. | $\sqrt{6}$ | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
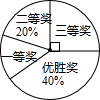 国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com