【题目】已知直线l经过A（6，0）和B（0，12）两点，且与直线y=x交于点C．

（1）求直线l的解析式；
（2）若点P（x，0）在线段OA上运动，过点P作l的平行线交直线y=x于D，求△PCD的面积S与x的函数关系式；S有最大值吗？若有，求出当S最大时x的值；

（3）若点P（x，0）在x轴上运动，是否存在点P，使得△PCA成为等腰三角形？若存在，请写出点P的坐标；若不存在，请说明理由．

参考答案：

【答案】
（1）

解：设直线L解析式为y=kx+b，

将A（6，0）和B（0，12）代入，得：

，

解得： ，

∴直线L解析式为y=﹣2x+12；


（2）

解：解方程组： ，

得： ，

∴点C的坐标为（4，4），

∴S△COP= x×4=2x；

∵PD∥l，

∴ ，

而 = ，

∴ ，

即 ，

∴△PCD的面积S与x的函数关系式为：

S=﹣ x2+2x，

∵S=﹣ （x﹣3）2+3，

∴当x=3时，S有最大值，最大值是3．


（3）

解：

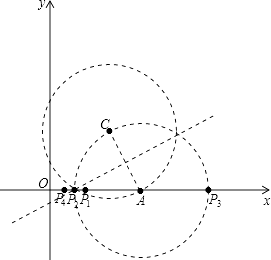
存在点P，使得△PCA成为等腰三角形，

∵点C的坐标为（4，4），A（6，0），

根据P1C=CA，P3A=AC，P2A=AC，P4C=P4A时分别求出即可，

当P1C=CA时，P1（2，0），

当P2A=AC时，P2（6﹣2 ，0），

当P3A=AC时，P3（6+2 ，0），

当P4C=P4A时，P4（1，0），

∴点P的坐标分别为：

P1（2，0），P2（6﹣2 ，0），P3（6+2 ，0），P4（1，0）．


【解析】（1）利用待定系数法将A（6，0）和B（0，12）代入解析式，求出即可；（2）将两函数解析式联立，得出点C的坐标，再利用平行线的性质，进而求出 ，再利用二次函数最值求出即可；（3）分别根据P1C=CA，P3A=AC，P2A=AC，P4C=P4A时结合图形求出即可．
【考点精析】本题主要考查了一次函数的图象和性质和二次函数的最值的相关知识点，需要掌握一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远；如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a才能正确解答此题．

关闭