
����Ŀ����֪����������y= ![]() ��ͼ���ڶ������ޣ�һ�κ���Ϊy=kx+b��b��0����ֱ��x=1��x�ύ�ڵ�B����ֱ��y=kx+b���ڵ�A��ֱ��x=3��x�ύ�ڵ�C����ֱ��y=kx+b���ڵ�D��
��ͼ���ڶ������ޣ�һ�κ���Ϊy=kx+b��b��0����ֱ��x=1��x�ύ�ڵ�B����ֱ��y=kx+b���ڵ�A��ֱ��x=3��x�ύ�ڵ�C����ֱ��y=kx+b���ڵ�D��
��1������A��D���ڵ�һ���ޣ���֤��b����3k��
��2���ڣ�1���������£���ֱ��y=kx+b��x�ύ�ڵ�E��y�ύ�ڵ�F���� ![]() =
= ![]() �ҡ�OFE���������
�ҡ�OFE��������� ![]() ʱ�������һ�κ����Ľ���ʽ����ֱ��д������ʽ
ʱ�������һ�κ����Ľ���ʽ����ֱ��д������ʽ ![]() ��kx+b�Ľ⼯��
��kx+b�Ľ⼯��
���𰸡�
��1��
֤�����߷���������y= ![]() ��ͼ���ڶ������ޣ�
��ͼ���ڶ������ޣ�
��k��0��
��һ�κ���Ϊy=kx+b��x���������С��
��A��D���ڵ�һ���ޣ�
��3k+b��0��
��b����3k
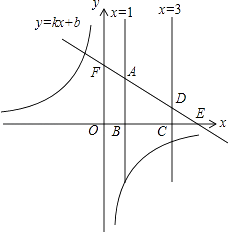
��2��
�⣺������֪�� ![]() ��
��
�� ![]() �٣�
�٣�
��E���� ![]() ��0����F��0��b����
��0����F��0��b����
��S��OEF= ![]() ������
������ ![]() ����b=
����b= ![]() �ڣ�
�ڣ�
�ɢ٢������������ã�k=�� ![]() ��b=3��
��b=3��
�����һ�κ����Ľ���ʽΪy=�� ![]() x+3��
x+3��
�⩁ ![]() =��
=�� ![]() x+3��x1=
x+3��x1= ![]() ��x2=
��x2= ![]() ��
��
��ֱ��y=kx+b�뷴��������y= ![]() �Ľ�������ĺ�������
�Ľ�������ĺ������� ![]() ��
�� ![]() ��
��
���ʽ ![]() ��kx+b�Ľ⼯Ϊ
��kx+b�Ľ⼯Ϊ ![]() ��x��0��x��
��x��0��x�� ![]() ��
��
����������1���ɷ���������y= ![]() ��ͼ���ڶ������ޣ��õ�k��0�����ǵõ�һ�κ���Ϊy=kx+b��x���������С������A��D���ڵ�һ���ޣ��õ�����ʽ���ɵõ����ۣ���2����������õ�
��ͼ���ڶ������ޣ��õ�k��0�����ǵõ�һ�κ���Ϊy=kx+b��x���������С������A��D���ڵ�һ���ޣ��õ�����ʽ���ɵõ����ۣ���2����������õ� ![]() ���������ε������ʽ�õ�S��OEF=
���������ε������ʽ�õ�S��OEF= ![]() ������
������ ![]() ����b=
����b= ![]() ������������k=��
������������k=�� ![]() ��b=3�����ɵõ����ۣ�
��b=3�����ɵõ����ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l����A��6��0����B��0��12�����㣬����ֱ��y=x���ڵ�C��
��1����ֱ��l�Ľ���ʽ��
��2������P��x��0�����߶�OA���˶�������P��l��ƽ���߽�ֱ��y=x��D�����PCD�����S��x�ĺ�����ϵʽ��S�����ֵ�����У������S���ʱx��ֵ��
��3������P��x��0����x�����˶����Ƿ���ڵ�P��ʹ�á�PCA��Ϊ���������Σ������ڣ���д����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����С����6�ű�����ȫ��ͬ��ֽ�ƽ���������Ϸ����Ϸ�������£�������ֱ��������1��3��6������ֽ�Ƹ�С����������ֱ��������2��4��5������ֽ�Ƹ�С����С��С���ֱ�ֽ�Ʊ��泯�ϣ��Ӹ��Ե�����ֽ����������һ�ţ�������������ſ�Ƭ�ϵ�������ӣ������Ϊż������С����ʤ�������Ϊ��������С����ʤ��
��1��С���鵽��������6��ֽ�Ƶĸ���Ϊ��
��2��������״ͼ���б��ķ�����С����ʤ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AB=2��EΪBC�е㣬��������M��N�ֱ��ڱ�CD��AD���˶���MN=1������ABE����D��M��NΪ��������������ƣ���DM= �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̫���ܹ���������ִ���ɫ��������֮һ�����������Լ��ݶ��Ľ��ɹ�����棬�Ľ�ǰ�ݶ������ABC��ͼ2��ʾ��BC=10�ף���ABC=��ACB=36�㣬�Ľ���D��BA���ӳ����ϣ��ҡ�BDC=90�㣬��Ľ���������������Ӳ���AD�ij����������ȷ��0.1�ף� ���ο����ݣ�sin18���0.31��cos18���0.95��tan18���0.32��sin36���0.59��cos36���0.81��tan36���0.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ھ���ABCD�У�BC��AB����BAD��ƽ����AF��BD��BC�ֱ��ڵ�E��F����O��BD���е㣬ֱ��OK��AF����AD�ڵ�K����BC�ڵ�G��
��1����֤���١�DOK�ա�BOG����AB+AK=BG��
��2����KD=KG��BC=4�� ![]() ��
��
����KD�ij��ȣ�
����ͼ2����P���߶�KD�ϵĶ��㣨�����D��K�غϣ���PM��DG��KG�ڵ�M��PN��KG��DG�ڵ�N����PD=m����S��PMN= ![]() ʱ����m��ֵ��
ʱ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O��ֱ��Ϊ10����AB�ij�Ϊ6��M����AB�ϵ�һ���㣬���߶ε�OM�ij���ȡֵ��Χ�ǣ� �� 
A.3��OM��5
B.4��OM��5
C.3��OM��5
D.4��OM��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�Һ���λ�ڵ���P�ı�ƫ��60�㷽�������86n mile��A�����������Ϸ�����һ��ʱ�����λ�ڵ���P����ƫ��45�㷽���ϵ�B������ʱ��B�������P�ľ���ԼΪ n mile�������ȡ�������ο����ݣ� ![]() ��1.7��
��1.7�� ![]() ��1.4��
��1.4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com