
【题目】综合与探究:如图,在平面直角坐标系中,Rt△AOC的直角边OC在y轴正半轴上,且顶点O与坐标原点重合,点A的坐标为(2,4),直线y=-x+b过点A,与x轴交于点B.
(1)求点B的坐标及直线AB的解析式;
(2)动点P从点O出发,以每秒1个单位长的速度,沿O-C-A的路线向点A运动,同时动点M从点B出发,以相同的速度沿BO的方向向O运动,过点M作MQ⊥x轴,交线段BA或线段AO于点Q,当点P到达A点时,点P和点M都停止运动.在运动过程中,设动点P运动的时间为t秒.△APQ的面积为S,求S关于t的函数关系式;
(3)是否存在以M、P、Q为顶点的三角形的面积与S相等?若存在,求t的值;若不存在,请说明理由.
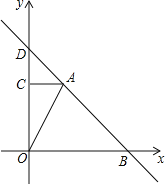
【答案】(1)点B的坐标为(6,0);直线AB的解析式为:y=-x+6;(2)S= ;(3)t=2或
;(3)t=2或![]() .
.
【解析】
(1)先将点A(2,4)代入y=-x+b,运用待定系数法求出直线AB的解析式,再令y=0,求出x的值,即可得到与x轴交点B的坐标;
(2)①先求出直线AB与y轴交点D的坐标,由B、D两点的坐标,可知△OBD是等腰直角三角形,再过点A作AN⊥OB于N,可得AN=OC=4,BN=AN=4,则当点P到达点C时,点M到达点N,所以分两种情况讨论:(i)当0≤t≤4,即点P在OC上,点Q在BA上时,用含t的代数式分别表示PQ、CP,再根据S=![]() PQCP即可求解;(ii)当4<t≤6,即点P在AC上,点Q在AO上时,延长MQ交AC于点E,用含t的代数式分别表示AP、QE,再根据S=
PQCP即可求解;(ii)当4<t≤6,即点P在AC上,点Q在AO上时,延长MQ交AC于点E,用含t的代数式分别表示AP、QE,再根据S=![]() APQE即可求解;
APQE即可求解;
②分两种情况讨论:(i)当0≤t≤4,即点P在OC上,点Q在BA上时,先由三角形面积公式求出S△MPQ=-![]() t2+3t,再根据S△MPQ=S=
t2+3t,再根据S△MPQ=S=![]() t2-5t+12列出方程,解方程即可;(ii)当4<t≤6,即点P在AC上,点Q在AO上时,先由三角形面积公式求出S△MPQ=(6-t)|10-2t|,再根据S△MPQ=S=(6-t)(t-4),列出方程,解方程即可.
t2-5t+12列出方程,解方程即可;(ii)当4<t≤6,即点P在AC上,点Q在AO上时,先由三角形面积公式求出S△MPQ=(6-t)|10-2t|,再根据S△MPQ=S=(6-t)(t-4),列出方程,解方程即可.
(1)将点A(2,4)代入y=-x+b,
得4=-2+b,解得b=6,
∴直线AB的解析式为:y=-x+6,
当y=0时,x=6,
∴点B的坐标为(6,0).
(2)设直线y=-x+6与y轴交于点D,则D(0,6),∵B(6,0),
∴OB=OD=6,∠OBD=∠ODB=45°.
过点A(2,4)作AN⊥OB于N,则AN=OC=4,ON=AC=2,BN=AN=4,

∴当点P到达点C时,点M到达点N.
分两种情况讨论:
(i)当0≤t≤4时,点P在OC上,点Q在BA上,如图1.
∵OP=t,BM=QM=t,
∴PQ∥OB,PQ=OM=OB-BM=6-t,CP=OC-OP=4-t,
∴S=![]() PQCP=
PQCP=![]() (6-t)(4-t)=
(6-t)(4-t)=![]() t2-5t+12;
t2-5t+12;
(ii)当4<t≤6时,点P在AC上,点Q在AO上,如图2,延长MQ交AC于点E.

∵OC+CP=t,BM=t,
∴AP=6-t,OM=OB-BM=6-t.
∵tan∠AON=![]() ,
,
∴![]() ,
,
∴QM=12-2t,
∴QE=EM-QM=4-(12-2t)=2t-8,
∴S=![]() APQE=
APQE=![]() (6-t)(2t-8)=-t2+10t-24.
(6-t)(2t-8)=-t2+10t-24.
综上可知,S= ;
;
②存在以M、P、Q为顶点的三角形的面积与S相等,理由如下:
分两种情况讨论:
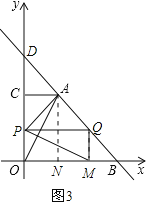
(i)当0≤t≤4时,点P在OC上,点Q在BA上,如图3.
∵S△MPQ=![]() PQQM=
PQQM=![]() (6-t)t=-
(6-t)t=-![]() t2+3t,S=
t2+3t,S=![]() t2-5t+12,
t2-5t+12,
∴-![]() t2+3t=
t2+3t=![]() t2-5t+12,
t2-5t+12,
整理,得t2-8t+12=0,
解得t1=2,t2=6(不合题意舍去);
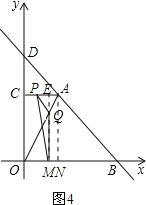
(ii)当4<t≤6时,点P在AC上,点Q在AO上,如图4.
∵QM=12-2t,PE=|CE-CP|=|(6-t)-(t-4)|=|10-2t|,
∴S△MPQ=![]() QMPE=
QMPE=![]() (12-2t)|10-2t|=(6-t)|10-2t|,
(12-2t)|10-2t|=(6-t)|10-2t|,
又∵S=![]() APQE=
APQE=![]() (6-t)(2t-8)=(6-t)(t-4),
(6-t)(2t-8)=(6-t)(t-4),
∴(6-t)|10-2t|=(6-t)(t-4),
∵t=6时,M与Q重合,不合题意舍去,
∴10-2t=±(t-4),
当10-2t=t-4时,t=![]() ;
;
当10-2t=-(t-4)时,t=6舍去.
综上可知,存在以M、P、Q为顶点的三角形的面积与S相等,此时t的值为2或![]() .
.


科目:初中数学 来源: 题型:
【题目】反比例函数![]() 的图象经过点
的图象经过点![]() 点是直线
点是直线![]() 上一个动点,如图所示,设
上一个动点,如图所示,设![]() 点的横坐标为
点的横坐标为![]() 且满足
且满足![]() 过
过![]() 点分别作
点分别作![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() 与双曲线分别交于
与双曲线分别交于![]() 两点,连结
两点,连结![]() .
.
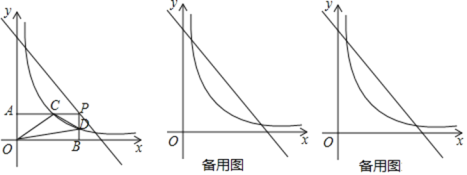
(1)求![]() 的值并结合图像求出
的值并结合图像求出![]() 的取值范围;
的取值范围;
(2)在![]() 点运动过程中,求线段
点运动过程中,求线段![]() 最短时点
最短时点![]() 的坐标;
的坐标;
(3)将三角形![]() 沿着
沿着![]() 翻折,点
翻折,点![]() 的对应点
的对应点![]() 得到四边形
得到四边形![]() 能否为菱形?若能,求出
能否为菱形?若能,求出![]() 点坐标;若不能,说明理由;
点坐标;若不能,说明理由;
(4)在![]() 点运动过程中使得
点运动过程中使得![]() 求出此时
求出此时![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
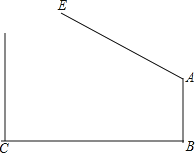
【题目】某公司大门出口处有一自动感应栏杆,点A是栏杆转动的支点,当车辆经过时,栏杆AE会自动升起,某天早上,栏杆发生故障,在某个位置突然卡住,这时测得栏杆升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大门BC打开的宽度为2米,这时一辆长宽高分别为(4600 mm、1700 mm、1400 mm)的汽车能否顺利通过?(栏杆宽度,汽车反光镜忽略不计,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12m。设AD的长为xm,DC的长为ym。
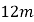
(1)求y与x之间的函数关系式;
(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣5,1),B(﹣2,2),C(﹣1,4),请按下列要求画图:
(1)将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
(2)画出与△ABC关于原点O成中心对称的△A2B2C2,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
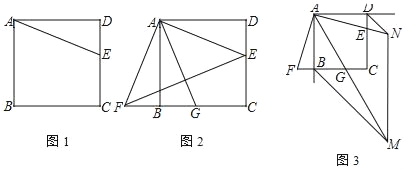
【题目】如图,点E是正方形ABCD中CD边上任意一点,AB=4,以点A为中心,把△ADE顺时针旋转90°得到△AD′F
(1)画出旋转后的图形,求证:点C、B、F三点共线;
(2)AG平分∠EAF交BC于点G.
①如图2,连接EF.若BG:CE=5:6,求△AEF的面积;
②如图3,若BM、DN分别为正方形的两个外角角平分线,交AG、AE的延长线于点M、N.当MM∥DC时,直接写出DN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
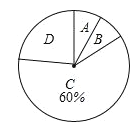
【题目】今年5月,某大型商业集团随机抽取所属的m家商业连锁店进行评估,将各连锁店按照评估成绩分成了A、B、C、D四个等级,绘制了如图尚不完整的统计图表.
评估成绩n(分) | 评定等级 | 频数 |
90≤n≤100 | A | 2 |
80≤n<90 | B | |
70≤n<80 | C | 15 |
n<70 | D | 6 |
根据以上信息解答下列问题:
(1)求m的值;
(2)在扇形统计图中,求B等级所在扇形的圆心角的大小;(结果用度、分、秒表示)
(3)从评估成绩不少于80分的连锁店中任选2家介绍营销经验,求其中至少有一家是A等级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,﹣3),点P是直线BC下方抛物线上的任意一点.
(1)求这个二次函数y=x2+bx+c的解析式.
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形POP′C,如果四边形POP′C为菱形,求点P的坐标.
(3)如果点P在运动过程中,能使得以P、C、B为顶点的三角形与△AOC相似,请求出此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过点(﹣1,0)和(m,0),且1<m<2,当x<﹣1时,y随着x的增大而减小.下列结论:
①abc>0;
②a+b>0;
③若点A(﹣3,y1),点B(3,y2)都在抛物线上,则y1<y2;
④a(m﹣1)+b=0;
⑤若c≤﹣1,则b2﹣4ac≤4a.
其中结论错误的是 .(只填写序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com