
【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,﹣3),点P是直线BC下方抛物线上的任意一点.
(1)求这个二次函数y=x2+bx+c的解析式.
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形POP′C,如果四边形POP′C为菱形,求点P的坐标.
(3)如果点P在运动过程中,能使得以P、C、B为顶点的三角形与△AOC相似,请求出此时点P的坐标.

【答案】(1)y=x2﹣2x﹣3(2)(2)(![]() ,-
,-![]() )(3)P、C、B为顶点的三角形与△AOC相似,此时点P的坐标(1,﹣4)
)(3)P、C、B为顶点的三角形与△AOC相似,此时点P的坐标(1,﹣4)
【解析】
(1)根据待定系数法,可得函数解析式;
(2)根据菱形的对角线互相垂直平分,可得P点的纵坐标,根据自变量与函数值的对应关系,可得答案;
(3)分类讨论:①当∠PCB=90°,根据互相垂直的两条直线的一次项系数互为负倒数,可得BP的解析式,根据自变量与函数值的对应关系,可得P点坐标;根据勾股定理,可得BC,CP的长,根据两组对边对应成比例且夹角相等的两个三角形相似,可得答案;
②当∠BPC=90°时,根据相似三角形的性质,可得P点的坐标,根据两组对边对应成比例且夹角相等的两个三角形相似,可得答案.
(1)将B、C点代入函数解析式,得:![]() ,解得:
,解得:![]() ,这个二次函数y=x2+bx+c的解析式为y=x2﹣2x﹣3;
,这个二次函数y=x2+bx+c的解析式为y=x2﹣2x﹣3;
(2)∵四边形POP′C为菱形,∴OC与PP′互相垂直平分,∴yP![]() ,即x2﹣2x﹣3
,即x2﹣2x﹣3![]() ,解得:x1
,解得:x1![]() ,x2
,x2![]() (舍),P(
(舍),P(![]() );
);
(3)∵∠PBC<90°,∴分两种情况讨论:
①如图1,当∠PCB=90°时,过P作PH⊥y轴于点H,BC的解析式为y=x﹣3,CP的解析式为y=﹣x﹣3,设点P的坐标为(m,﹣3﹣m),将点P代入代入y═x2﹣2x﹣3中,解得:m1=0(舍),m2=1,即P(1,﹣4);
AO=1,OC=3,CB![]() ,CP
,CP![]() ,此时
,此时![]() 3,△AOC∽△PCB;
3,△AOC∽△PCB;
②如图2,当∠BPC=90°时,作PH⊥y轴于H,作BD⊥PH于D.
∵PC⊥PB,∴△PHC∽△BDP,∴![]() .设点P的坐标为(m,m2﹣2m﹣3),则PH=m,HC=-(m2﹣2m﹣3)-(-3)=-m2+2m,BD=-(m2﹣2m﹣3),PD=3-m,∴
.设点P的坐标为(m,m2﹣2m﹣3),则PH=m,HC=-(m2﹣2m﹣3)-(-3)=-m2+2m,BD=-(m2﹣2m﹣3),PD=3-m,∴![]() ,∴
,∴![]() ,解得:m
,解得:m![]() 或
或![]() (舍去).当m
(舍去).当m![]() 时,m2﹣2m﹣3=
时,m2﹣2m﹣3=![]() .
.
∵△PHC∽△BDP,∴![]() =
=![]() =
=![]()
![]() 3,以P、C、B为顶点的三角形与△AOC不相似.
3,以P、C、B为顶点的三角形与△AOC不相似.
综上所述:P、C、B为顶点的三角形与△AOC相似,此时点P的坐标(1,﹣4).


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线y=3x﹣3分别交x轴、y轴于A、B两点,抛物线y=x2+bx+c经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
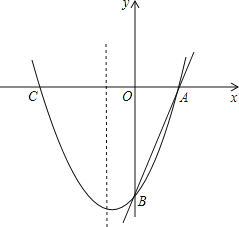
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究:如图,在平面直角坐标系中,Rt△AOC的直角边OC在y轴正半轴上,且顶点O与坐标原点重合,点A的坐标为(2,4),直线y=-x+b过点A,与x轴交于点B.
(1)求点B的坐标及直线AB的解析式;
(2)动点P从点O出发,以每秒1个单位长的速度,沿O-C-A的路线向点A运动,同时动点M从点B出发,以相同的速度沿BO的方向向O运动,过点M作MQ⊥x轴,交线段BA或线段AO于点Q,当点P到达A点时,点P和点M都停止运动.在运动过程中,设动点P运动的时间为t秒.△APQ的面积为S,求S关于t的函数关系式;
(3)是否存在以M、P、Q为顶点的三角形的面积与S相等?若存在,求t的值;若不存在,请说明理由.
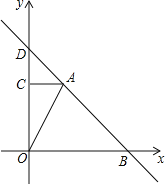
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.
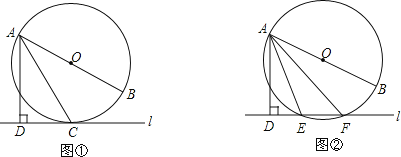
(1)如图①,当直线l与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图②,当直线l与⊙O相交于点E、F时,若∠DAE=18°,求∠BAF的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
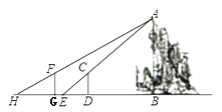
【题目】假山具有多方面的造景功能,与建筑、植物等组合成富于变化的景致.某公园有一座假山,小亮、小慧等同学想用一些测量工具和所学的几何知识测量这座假山的高度来检验自己掌握知识和运用知识的能力,如图,在阳光下,小亮站在水平地面的D处,此时小亮身高的影子顶端与假山的影子顶端E重合,这时小亮身高CD的影长DE=2米,一段时间后,小亮从D点沿BD的方向走了3.6米到达G处,此时小亮身高的影子顶端与假山的影子顶端H重合,这时小亮身高的影长GH=2.4米,已知小亮的身高CD=FG=1.5米,点G,E,D均在直线BH上,AB⊥BH,CD⊥BH,GF⊥BH,请你根据题中提供的相关信息,求出假山的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】假期,六盘水市教育局组织部分教师分别到A.B.C.D四个地方进行新课程培训,教育局按定额购买了前往四地的车票.如图1是未制作完成的车票种类和数量的条形统计图,请根据统计图回答下列问题:
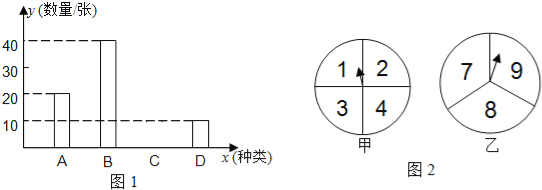
(1)若去C地的车票占全部车票的30%,则去C地的车票数量是 张,补全统计图.
(2)若教育局采用随机抽取的方式分发车票,每人一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么余老师抽到去B地的概率是多少?
(3)若有一张去A地的车票,张老师和李老师都想要,决定采取旋转转盘的方式来确定.其中甲转盘被分成四等份且标有数字1、2、3、4,乙转盘分成三等份且标有数字7、8、9,如图2所示.具体规定是:同时转动两个转盘,当指针指向的两个数字之和是偶数时,票给李老师,否则票给张老师(指针指在线上重转).试用“列表法”或“树状图”的方法分析这个规定对双方是否公平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通信公司策划了![]() 两种上网的月收费方式:
两种上网的月收费方式:
收费方式 | 月使用费/元 | 包时上网时间/ | 超时费/(元/ |
| 30 | 25 | 0.05 |
|
|
|
|
设每月上网时间为![]() ,方式
,方式![]() 的收费金额分别为
的收费金额分别为![]() (元),
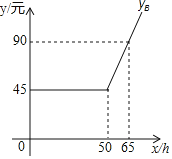
(元),![]() (元),如图是
(元),如图是![]() 与
与![]() 之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
之间函数关系的图象.(友情提示:若累计上网时间不超出包时上网时间,则只收月使用费;若累计上网时间超出包时上网时间,则对超出部分再加收超时费)
(1)![]() ,
,![]() ,
,![]() ;
;
(2)求![]() 之间的函数解析式;
之间的函数解析式;
(3)若每月上网时间为31小时,请直接写出选择哪种方式能节省上网费.
查看答案和解析>>
科目:初中数学 来源: 题型:
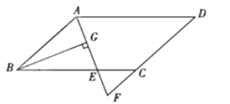
【题目】如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=![]() ,则△EFC的面积是( )
,则△EFC的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC=4,以点A为圆心,2为半径的⊙A与BC相切于点D,交AB于点E,交AC于点F,点P是⊙A上的一点,且∠EPF=45°,则图中阴影部分的面积为( )

A. 4﹣2π B. 8+π C. 4﹣π D. 8﹣2π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com