
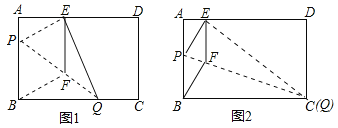
【题目】如图1,在矩形纸片![]() 中,
中,![]() ,
,![]() ,折叠纸片使点
,折叠纸片使点![]() 落在
落在![]() 上的点
上的点![]() 处,折痕为
处,折痕为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
(1)求证:四边形![]() 为菱形;
为菱形;
(2)当折痕![]() 的点
的点![]() 与点
与点![]() 重合时(如图2),求菱形
重合时(如图2),求菱形![]() 的边长.
的边长.
【答案】(1)见解析;(2)边长为![]() .
.
【解析】
(1)根据一组对边平行且相等可证得:四边形BFEP为平行四边形,再加上PB=PE可得结论;
(2)先由折叠得:EC=BC=AD=5,利用勾股定理得:ED=4,设PE=x,则PB=x,AP=3-x,Rt△APE中,由勾股定理得:![]() ,解出即可;
,解出即可;
(1)证明:有题意可知:
∵点![]() 与点
与点![]() 关于
关于![]() 对称,
对称,
![]() ,
,![]()
∵![]()
∴![]()
∴∠BPF=![]()
∴![]()
∴![]()
∴四边形BFED是平行四边形,
∵![]()
∴四边形![]() 为菱形;
为菱形;
(2)如图,当点![]() 与点
与点![]() 重合时,
重合时,
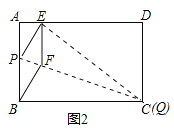
由折叠可知:EC=BC=AD=5,
∵在直角△CDE中,CD=AB=3,
∴![]() ,
,
∴AE=1,
设PE=x,则PB=x,AP=3-x,
Rt△APE中,由勾股定理得:![]() ,
,
解得:![]() ,
,
即菱形![]() 的边长PB=
的边长PB=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).

(1)四边形EFGH是什么四边形?证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形;
(3)你学过的哪种特殊四边形的中点四边形是矩形? . (填一种即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 上的点,
上的点,![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有( )
.其中正确的结论有( )
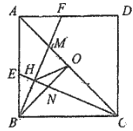
A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
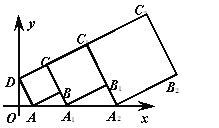
【题目】在平面坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2018个正方形的面积为( )
A. 5·![]() B. 5·
B. 5·![]() C. 5·
C. 5·![]() D. 5·
D. 5·![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
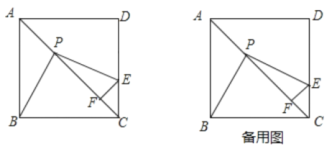
【题目】已知如图,边长为2的正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一个动点(与点
上的一个动点(与点![]() 、
、![]() 不重合),过点
不重合),过点![]() 作
作![]() ,
,![]() 交射线
交射线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.
(1)求证:![]() :
:
(2)在点![]() 的运动过程中,
的运动过程中,![]() 的长度是否发生变化?若不变,试求出这个不变的值,写出解答过程:若变化,试说明理由:
的长度是否发生变化?若不变,试求出这个不变的值,写出解答过程:若变化,试说明理由:
(3)在点![]() 的运动过程中,
的运动过程中,![]() 能否为等腰三角形?如果能,直接写出此时
能否为等腰三角形?如果能,直接写出此时![]() 的长;如果不能,试说明理由.
的长;如果不能,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
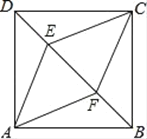
【题目】如图,正方形ABCD中,点E,F是对角线BD上两点,DE=BF.
(1)判断四边形AECF是什么特殊四边形,并证明;
(2)若EF=4,DE=BF=2,求四边形AECF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
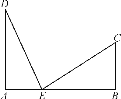
【题目】如图,铁路上A,B两点相距25 km,C,D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=15 km,CB=10 km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等,则E站应建在离A站多少km处?
查看答案和解析>>
科目:初中数学 来源: 题型:
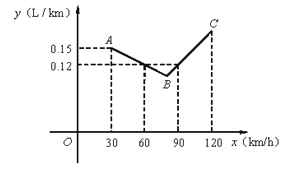
【题目】图中的折线![]() 表示某汽车的耗油量
表示某汽车的耗油量![]() (单位:
(单位:![]() )与速度
)与速度![]() (单位:
(单位:![]() )之间的函数关系(
)之间的函数关系(![]() ),已知线段
),已知线段![]() 表示的函数关系中,该汽车的速度每增加
表示的函数关系中,该汽车的速度每增加![]() ,耗油量增加
,耗油量增加![]() .
.
(1) 当速度为![]() 、
、![]() 时,该汽车的耗油量分别为_____
时,该汽车的耗油量分别为_____![]() 、____
、____![]() ;
;
(2) 速度是多少时,该汽车的耗油量最低?最低是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com