Question

【题目】直线MN与线段AB相交于点O．点C，点D分别为射线ON，OM上两点，且满足∠ACN=∠ODB=45°．

【特殊发现】

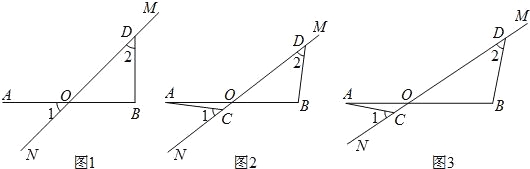
（1）如图1，若AO=OB，当点C与点O重合时，此时AO与BD的数量关系为 ，AO与BD的位置关系为 ；

【拓展探究】

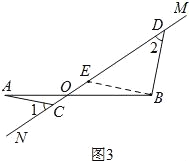
（2）将图1中的MN绕点O顺时针旋转α°，（0＜α＜45），如图2所示，若AO=OB，求证：AC=BD，AC⊥BD；

【解决问题】

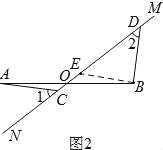
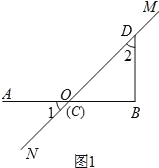
（3）如图3，若kAO=OB，求的值．

Answer 1

【答案】（1）AO=BD，AO⊥BD；

（2）证明见解析；

（3）k．

【解析】

试题分析：（1）先根据∠BOD和∠2的度数，判断DB与OB的数量关系以及位置关系，再得出AO与BD的数量关系与位置关系；

（2）先过点B作BE∥AC，通过判定△AOC≌△BOE，得到∠BED的度数，再根据∠BED和∠2的度数，判断DB与EB的数量关系以及位置关系，再得出AC与BD的数量关系与位置关系；

（3）先过点B作BE∥AC，根据△AOC∽△BOE，得出BE与AC的比值，再根据DB=BE，得出BD与AC的比值．

试题解析：（1）如图1，当点C与点O重合时，∠1=∠DOB=45°

∵∠2=45°

∴DB=OB，且∠B=90°，即△BOD是等腰直角三角形

又∵AO=OB

∴AO=BD

∵∠B=90°

∴DB⊥AB，即DB⊥AO

故答案为：AO=BD；AO⊥BD

（2）如图2，过点B作BE∥AC，交MN于E，则∠A=∠OBE

∵AO=BO，∠AOC=∠BOE

∴△AOC≌△BOE（ASA）

∴AC=BE，∠ACO=∠BEO

∴∠1=∠BED=45°

又∵∠2=45°

∴∠DBE=90°，且DB=BE，即△BED是等腰直角三角形

∴DB⊥BE，AC=DB

又∵BE∥AC

∴AC⊥BD

（3）如图3，过点B作BE∥AC，交MN于E，则△AOC∽△BOE

∴=k，且∠ACO=∠BEO

∴∠1=∠BED=45°

又∵∠2=45°

∴DB=BE

∴=k