
【题目】如图1,在△ABC中,∠ABC=90°,AO是△ABC的角平分线,以O为圆心,OB为半径作圆交BC于点D,
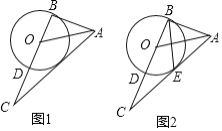
(1)求证:直线AC是⊙O的切线;
(2)在图2中,设AC与⊙O相切于点E,连结BE,如果AB=4,tan∠CBE=![]() .
.
①求BE的长;②求EC的长.
【答案】(1)见解析;(2)①![]() ;②
;②![]() .
.
【解析】
(1)作作OE⊥AC,由AO是∠BAC的角平分线,得到∠BAO=∠EAO,判断出△ABO≌△AEO(AAS),得到OE=OB,所以直线AC是⊙O的切线;
(2)先利用AE与⊙O相切于点E, AB=AE=4,再用三角函数求出OB,BC,然后用三角形相似,得到BC=2CE,![]() ,用勾股定理求出CD,最后用切割线定理即可
,用勾股定理求出CD,最后用切割线定理即可
证明:(1)如图1,
作OE⊥AC, ∴∠OEA=90°,
∵∠ABC=90,∴∠OEA=∠ABC,
∵AO是△ABC的角平分线,∴∠BAO=∠EAO,
在△ABO和△AEO中,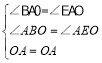 ,
,
∴△ABO≌△AEO(AAS),∴OE=OB,
∵OB是⊙O的半径,∴OE是⊙O的半径, ∴直线AC是⊙O的切线;
(2)①如图2,∵∠ABO=90°,

∴AB切⊙O于B,
∵AE与⊙O相切于点E, ∴AB=AE=4,
∵AO是△ABC的角平分线, ∴AO⊥BE, ∴∠BAO+∠ABE=90°,
∵∠CBE+∠ABE=90°, ∴∠BAO=∠CBE,
∵tan∠CBE=![]() , ∴tan∠BAO=
, ∴tan∠BAO=![]() ,
,
在Rt△ABO中,AB=4,tan∠BAO=![]() , ∴
, ∴![]() , ∴BD=2OB=4,
, ∴BD=2OB=4,
∵AB是⊙O的直径, ∴∠BED=90°,
又∵tan∠CBE=![]() =
=![]() , ∴BE=2DE,
, ∴BE=2DE,
在Rt△BDE中, ∵BE2+DE2=BD2, ∴![]() , 解得
, 解得![]() ;
;
②∵AC是⊙O的切线, ∴∠CED=∠CBE,
∵∠DCE=∠ECB,∴△CDE∽△CEB, ∴![]() ,
,
又∵tan∠CBE=![]() =
=![]() , ∴BC=2CE,
, ∴BC=2CE,![]() ,
,
∵BD=BC﹣CD ∴![]() , 解得
, 解得![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有四个分别标有1、2、3、4的小球,它们的形状、大小等完全相同.小黑先从口袋里随机不放回地取出一个小球,记下数字为x;小白在剩下有三个小球中随机取出一个小球,记下数字y.
(1)计算由x、y确定的点(x,y)在函数![]() 图象上的概率;
图象上的概率;
(2)小黑、小白约定做一个游戏,其规则是:若x、y满足xy>6,则小黑胜;若x、y满足xy<6,则小白胜.这个游戏规则公平吗?说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 轴于点(1,0),直线
轴于点(1,0),直线![]() 轴于点(2,0),直线
轴于点(2,0),直线![]() 轴于点(3,0),…,直线
轴于点(3,0),…,直线![]() 轴于点(n,0)。函数
轴于点(n,0)。函数![]() 的图象与直线
的图象与直线![]() 分别交于点
分别交于点![]() ;函数
;函数![]() 的图象与直线
的图象与直线![]() 分别交于点
分别交于点![]() 。如果
。如果![]() 的面积记作
的面积记作![]() ,四边形
,四边形![]() 的面积记作
的面积记作![]() ,四边形
,四边形![]() 的面积记作
的面积记作![]() ,…,四边形
,…,四边形![]() 的面积记作
的面积记作![]() ,那么
,那么![]() _____________.
_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是圆O的直径,O为圆心,AD、BD是半圆的弦,且∠PDA=∠PBD.延长PD交圆的切线BE于点E
(1)证明:直线PD是⊙O的切线.
(2)如果∠BED=60°,![]() ,求PA的长.
,求PA的长.
(3)将线段PD以直线AD为对称轴作对称线段DF,点F正好在圆O上,如图2,求证:四边形DFBE为菱形.
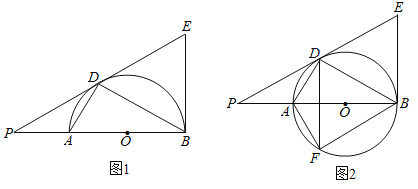
查看答案和解析>>
科目:初中数学 来源: 题型:
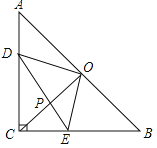
【题目】如图,在等腰直角△ABC中,∠ACB=90°,CO⊥AB于点O,点D、E分别在边AC、BC上,且AD=CE,连结DE交CO于点P,给出以下结论:
①△DOE是等腰直角三角形;②∠CDE=∠COE;③若AC=1,则四边形CEOD的面积为![]() ;④
;④![]() ,其中所有正确结论的序号是 .
,其中所有正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
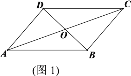
【题目】我们把有两边对应相等,且夹角互补(不相等)的两个三角形叫做“互补三角形”,如图1,□ABCD中,△AOB和△BOC是“互补三角形”.
(1)写出图1中另外一组“互补三角形”_______;
(2)在图2中,用尺规作出一个△EFH,使得△EFH和△EFG为“互补三角形”,且△EFH和△EFG在EF同侧,并证明这一组“互补三角形”的面积相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
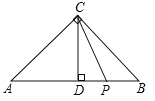
【题目】如图,在△ABC中,∠ACB=90°,∠A=45°,CD⊥AB于点D,点P在线段DB上,若AP2-PB2=48,则△PCD的面积为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垃圾的分类处理与回收利用,可以减少污染,节省资源.某城市环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况,其相关信息如下:

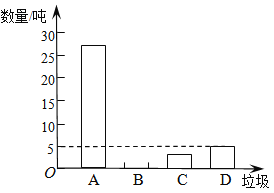
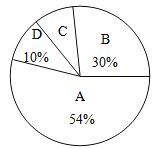
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在抽样数据中,产生的有害垃圾共 吨;
(3)调查发现,在可回收物中塑料类垃圾占![]() ,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
,每回收1吨塑料类垃圾可获得0.7吨二级原料.假设该城市每月产生的生活垃圾为5 000吨,且全部分类处理,那么每月回收的塑料类垃圾可以获得多少吨二级原料?
查看答案和解析>>
科目:初中数学 来源: 题型:
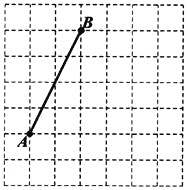
【题目】线段AB在由边长为1的小正方形组成的网格中,端点A、B为格点(即网格线的交点).
(1)线段AB的长度为________;
(2)在网格中找出一个格点C,使得△ABC是以AB为直角边的等腰直角三角形,请画出△ABC;
(3)在网格中找出一个格点D,使得△ABD是以AB为斜边的等腰直角三角形,请画出△ABD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com