
【题目】如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据: ![]() ≈1.732)
≈1.732)
【答案】解:如图,过点C作CD⊥AB于点D,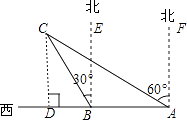
AB=20×1=20(海里),
∵∠CAF=60°,∠CBE=30°,
∴∠CBA=∠CBE+∠EBA=120°,∠CAB=90°﹣∠CAF=30°,
∴∠C=180°﹣∠CBA﹣∠CAB=30°,
∴∠C=∠CAB,
∴BC=BA=20(海里),
∠CBD=90°﹣∠CBE=60°,
∴CD=BCsin∠CBD= ![]() ≈17(海里).
≈17(海里).
【解析】过点C作CD⊥AB于点D,则若该船继续向西航行至离灯塔距离最近的位置为CD的长度,利用锐角三角函数关系进行求解即可.
【考点精析】利用锐角三角函数的定义对题目进行判断即可得到答案,需要熟知锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】早晨,小明步行到离家900米的学校去上学,到学校时发现眼镜忘在家中,于是他立即按原路步行回家,拿到眼镜后立即按原路骑自行车返回学校.已知小明步行从学校到家所用的时间比他骑自行车从家到学校所用的时间多10分钟,小明骑自行车速度是步行速度的3倍.
(1)求小明步行速度(单位:米/分)是多少;
(2)下午放学后,小明骑自行车回到家,然后步行去图书馆,如果小明骑自行车和步行的速度不变,小明步行从家到图书馆的时间不超过骑自行车从学校到家时间的2倍,那么小明家与图书馆之间的路程最多是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,点A坐标为(0,1),点B坐标为(0,﹣2),反比例函数y= ![]() 的图象经过点C,一次函数y=ax+b的图象经过A,C两点.
的图象经过点C,一次函数y=ax+b的图象经过A,C两点. 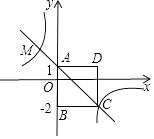
(1)求反比例函数与一次函数的解析式;
(2)若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个横断面为抛物线形状的拱桥,当水面宽4m时,拱顶(拱桥洞的最高点)离水面2m,当水面下降1m时,水面的宽度为( )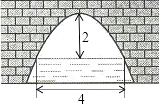
A.3
B.2 ![]()
C.3 ![]()
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
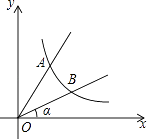
【题目】如图,直线y=2x与反比例函数y= ![]() (k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα=
(k≠0,x>0)的图象交于点A(1,a),B是反比例函数图象上一点,直线OB与x轴的夹角为α,tanα= ![]() .
.
(1)求k的值.
(2)求点B的坐标.
(3)设点P(m,0),使△PAB的面积为2,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=900,∠B=∠E=300.
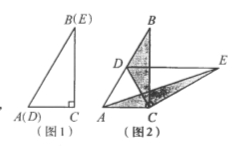


(1)操作发现如图2,固定△ABC,使△DEC绕点C旋转。当点D恰好落在BC边上时,填空:线段DE与AC的位置关系是 ;
② 设△BDC的面积为S1,△AEC的面积为S2。则S1与S2的数量关系是 。
(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC,CE边上的高,请你证明小明的猜想。
(3)拓展探究
已知∠ABC=600,点D是其角平分线上一点,BD=CD=4,OE∥AB交BC于点E(如图4),若在射线BA上存在点F,使S△DCF =S△BDC,请直接写出相应的BF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某青春党支部在精准扶贫活动中,给结对帮扶的贫困家庭赠送甲、乙两种树苗让其栽种.已知乙种树苗的价格比甲种树苗贵10元,用480元购买乙种树苗的棵数恰好与用360元购买甲种树苗的棵数相同.
(1)求甲、乙两种树苗每棵的价格各是多少元?
(2)在实际帮扶中,他们决定再次购买甲、乙两种树苗共50棵,此时,甲种树苗的售价比第一次购买时降低了10%,乙种树苗的售价不变,如果再次购买两种树苗的总费用不超过1500元,那么他们最多可购买多少棵乙种树苗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角△ABC中,∠BAC=90![]() ,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM.下列结论:①AE=AF;②AM⊥EF;③AF=DF;④DF=DN,其中正确的结论有( )
,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM.下列结论:①AE=AF;②AM⊥EF;③AF=DF;④DF=DN,其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com