
����Ŀ��һ�����������۳ɱ�Ϊ20Ԫ/ǧ�˵�ij��Ʒ��������۲��Ź涨���ò�Ʒÿǧ���ۼ۲��ó���90Ԫ�������۹����з��ֵ�����y��ǧ�ˣ����ۼ�x��Ԫ/ǧ�ˣ�����һ�κ�����ϵ����Ӧ��ϵ���±���
�ۼ�x��Ԫ/ǧ�ˣ� | �� | 50 | 60 | 70 | 80 | �� |
������y��ǧ�ˣ� | �� | 100 | 90 | 80 | 70 | �� |
��1����y��x�ĺ�����ϵʽ��
��2����������������4000Ԫ������Ӧ���ۼ۶�Ϊ����Ԫ��
��3���ò�Ʒÿǧ���ۼ�Ϊ����Ԫʱ�������̻�õ�����w��Ԫ�����ʱ���������Ϊ����Ԫ��
���𰸡�
��1��
�⣺��y��x�ĺ�����ϵʽΪy=kx+b��k��0�������������
![]() ��
��
��� ![]() ��
��
��y��x�ĺ�����ϵʽΪy=��x+150��
��2��
�⣺���������
����x+150����x��20��=4000��
���x1=70��x2=100��90���������⣬��ȥ����
�ʸ�������������4000Ԫ������Ӧ���ۼ۶�Ϊ70Ԫ��
��3��
�⣺w��x�ĺ�����ϵʽΪ��
w=����x+150����x��20��
=��x2+170x��3000
=����x��85��2+4225��
�ߩ�1��0��
�൱x=85ʱ��wֵ���w���ֵ��4225��
��ò�Ʒÿǧ���ۼ�Ϊ85Ԫʱ�������̻�õ�����w��Ԫ�����ʱ���������Ϊ4225Ԫ��
����������1������ͼ���еĸ����ɵó�y��x��һ�κ�����ϵ���Ӷ����ͼ�������ɵó�y��x�Ĺ�ϵʽ����2����������4000Ԫ�������г�������⼴�ɣ���3�����������̻�õ�������w��Ԫ��=������ÿ������ɱ�ʾ��w��x֮��ĺ�������ʽ�������ö��κ�������ֵ�ɵó��������ֵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У���֪��ABC�ա�FDE����A�������Ϊ��a��1����BC��x�ᣬB�������Ϊ��b��-2����D��E���㶼��y���ϣ���F�㵽y��ľ���Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A�Ƿ���������y1= ![]() ��x��0��ͼ����һ�㣬����A��x���ƽ���ߣ�������������y2=
��x��0��ͼ����һ�㣬����A��x���ƽ���ߣ�������������y2= ![]() ��x��0����ͼ���ڵ�B������OA��OB������OAB�����Ϊ2����k��ֵΪ ��
��x��0����ͼ���ڵ�B������OA��OB������OAB�����Ϊ2����k��ֵΪ �� 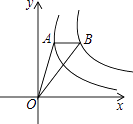
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧ��ѧϰ��ȫ�������ε����֪ʶ���֣�ֻ��������ȫ��ͬ�ij�����ֱ�߾Ϳ�������һ���ǵ�ƽ���ߣ���ͼ��һ��ֱ��ѹס����OB����һ��ֱ��ѹס����OA�������һ��ֱ�߽��ڵ�P��С��˵��������OP���ǡ�BOA�Ľ�ƽ���ߣ�������������������(����)

A. �ǵ��ڲ����ǵ����ߵľ�����ȵĵ��ڽǵ�ƽ������
B. ��ƽ�����ϵĵ㵽��������ߵľ������
C. ������������ƽ���ߵĽ��㵽�����ߵľ������
D. ���Ͼ�����ȷ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCDΪ�����Σ���A������Ϊ��0��1������B������Ϊ��0����2��������������y= ![]() ��ͼ����C��һ�κ���y=ax+b��ͼ��A��C���㣮
��ͼ����C��һ�κ���y=ax+b��ͼ��A��C���㣮
��1������������һ�κ����Ľ���ʽ��
��2������������һ�κ�������һ������M�����ꣻ
��3������ͼ��д��ʹһ�κ�����ֵ���ڷ�����������ֵ��x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y= ![]() ��ͼ���㣨2��3������ô�����ĸ����У�Ҳ���������ͼ���ϵ��ǣ� ��
��ͼ���㣨2��3������ô�����ĸ����У�Ҳ���������ͼ���ϵ��ǣ� ��
A.����6��1��
B.��1��6��
C.��2����3��
D.��3����2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�洬�ں����ϳ�����������20����/ʱ���ٺ��У���A���۲����C�ڱ�ƫ��60�㷽���ϣ�����1Сʱ����B������ʱ�۲쵽����C�ڱ�ƫ��30�㷽���ϣ����ô�����������������������������λ�ã����ʱ�洬�������ľ��루�����ȷ��1����ο����ݣ� ![]() ��1.732��
��1.732��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������ͬѧ��һ����Ƶ��ȥ���Ƹ��ʵ�ʵ���У�ͳ����ijһ������ֵ�Ƶ�ʻ����ͳ��ͼ��ͼ��ʾ���������һ�����ʵ������ǣ� ��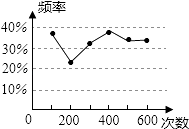
A.��һö������������ӣ�����1��ĸ���
B.��һ��װ��2�������1������Ĵ�������ȡһ��ȡ������ĸ���
C.��һöӲ�ң���������ĸ���
D.����дһ�����������ܱ�2�����ĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��BD�ǡ�ABC��ƽ���ߣ�DE��CB����AB�ڵ�E����A��45�㣬��BDC��60��.����BDE���ڽǵĶ�����
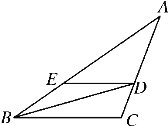
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com