
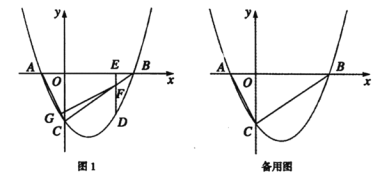
【题目】如图1,抛物线![]()
![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
(1)求该抛物线的函数表达式;
(2)动点![]() 在线段
在线段![]() 下方的抛物线上.
下方的抛物线上.
①连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,交
,交![]() 于点
于点![]() .过点
.过点![]() 作
作![]() ,垂足为
,垂足为![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() ;
;
②过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .是否存在点
.是否存在点![]() ,使得
,使得![]() 中的一个角恰好等于
中的一个角恰好等于![]() 的2倍?如果存在,求出点
的2倍?如果存在,求出点![]() 的横坐标;如果不存在,请说明理由.
的横坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②存在,1或
;②存在,1或![]()
【解析】
(1)根据题意可求点A(-1,0),点B(m,0),根据OB=3OA,可求m的值,即可求解析式;
(2)①先求出直线BC解析式,即可得F点坐标,利用![]() 可得用含t的代数式表示d;
可得用含t的代数式表示d;
②分∠CDH=2∠ABC或∠DCH=2∠ABC两种情况讨论,利用锐角三角函数,相似三角形的性质可求点D的横坐标.
解:(1)令y=0,则![]() ,
,
∴![]() ,
,
∴(x-m)(x+1)=0
∴![]()
∵m>0,点A在点B的左侧
∴点A(-1,0),点B(m,0)
∴OA=1,OB=m ,
∵OB=3OA ,∴m=3
∴抛物线![]()
(2)①如图1:连接AF
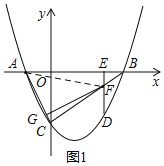
∵抛物线![]() 与y轴交与点C
与y轴交与点C
∴点C(0,-2)
∵点A(-1,0),点B(3,0),点C(0,-2)
∴AB=4,OC=2,AC=![]()
∵设直线BC解析式y=kx+b
∴![]()
解得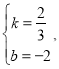
∴直线BC解析式![]()
∵D点横坐标为t,DF⊥AB
∴点F的横坐标为t ∴![]()
∵![]()
∴![]() ,
,
∴ ![]()
∴![]() ,
,
②若∠DCH=2∠ABC,如图2:
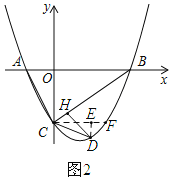
过点C作CF∥AB,交抛物线于F点,作DE⊥CF于点E.
∵AB∥CF ∴∠ABC=∠BCF
又∵∠DCH=2∠BCF
∴∠DCF=∠ABC=∠BCF
∵点D坐标为![]() ,
,
∴CE=t,DE=![]()
∵tan∠DCF=tan∠ABC= ![]()
∴ 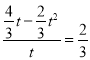
∴![]() (不合题意舍去),
(不合题意舍去),![]()
即点D的横坐标为1.
若∠CDH=2∠ABC,如图3:
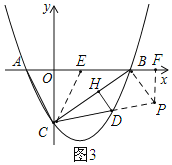
作∠ECB=∠ABC,过点B作BP∥HD,交CD的延长线于点P,作PF⊥AB于F.
∵∠ECB=∠ABC ∴EC=BE,∠AEC=2∠ABC ,
在Rt△OEC中,![]()
∴![]()
![]()
∴CE=![]() ,
,
∴OE=OB-BE=![]() ,
,
∴tan∠AEC=tan2∠ABC=![]()
∵点B(3,0),点C(0,-2)
∴BC=![]()
∵BP∥HD,HD⊥BC ∴BP⊥BC,∠CDH=∠CPB=2∠ABC
∴tan∠CPB=tan2∠ABC=![]() =
=![]() .
.
∴BP=![]()
∵∠ABC+∠PBF=90°,∠ABC+∠OCB=90° ,
∴∠OCB=∠PBF,且∠BOC=∠PFB=90°
∴△BOC∽△PFB ∴ 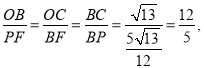
∴PF=![]() BF=
BF=![]()
∴![]()
∴点P坐标![]()
∵点C(0,-2),点P![]()
∴直线PC解析式![]()
∵直线CP与抛物线交于C,D两点
∴ 
解得:![]()
∴点D的横坐标为![]()
综上所述:点D的横坐标为![]() 或1
或1


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:
【题目】如图,小明想测量电线杆AB的高度,但在太阳光下,电线杆的影子恰好落在地面和土地的坡面上,量得坡面上的影长CD=4m,地面上的影长BC=10m,土坡坡面与地面成30°的角,此时测得1m长的木杆的影长为2m,求电线杆的高度.(结果精确到0.1m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB中点,AE∥CD,CE∥AB.
(1)试判断四边形ADCE的形状,并证明你的结论.
(2)连接BE,若∠BAC=30°,CE=1,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司经过市场调查,发现某种运动服的销量与售价是一次函数关系,具体信息如下表:
售价(元/件) | 200 | 210 | 220 | 230 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件150元.
(1)售价为![]() 元,月销量为
元,月销量为![]() 件;
件;
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②若销售该运动服的月利润为![]() 元,求
元,求![]() 关于
关于![]() 的函数关系式,并求月利润最大时的售价;
的函数关系式,并求月利润最大时的售价;
(2)由于运动服进价降低了![]() 元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则
元,商家决定回馈顾客,打折销售,这时月销量与调整后的售价仍满足(1)中函数关系式.结果发现,此时月利润最大时的售价比调整前月利润最大时的售价低15元,则![]() 的值是多少?
的值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初一(1)班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目),并根据调查结果列出统计表,绘制成扇形统计图.

根据以上信息解决下列问题:
(1)![]() ,
,![]() ;
;
(2)扇形统计图中机器人项目所对应扇形的圆心角度数为 ![]() ;
;
(3)从选航模项目的![]() 名学生中随机选取
名学生中随机选取![]() 名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的
名学生参加学校航模兴趣小组训练,请用列举法(画树状图或列表)求所选取的![]() 名学生中恰好有
名学生中恰好有![]() 名男生、
名男生、![]() 名女生的概率.
名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
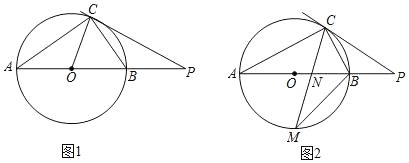
【题目】已知,AB是⊙O的直径,点C在⊙O上,点P是AB延长线上一点,连接CP.
(1)如图1,若∠PCB=∠A.
①求证:直线PC是⊙O的切线;
②若CP=CA,OA=2,求CP的长;
(2)如图2,若点M是弧AB的中点,CM交AB于点N,MNMC=9,求BM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店准备购进A、B两种品牌的文具袋进行销售,若购进A品牌文具袋和B品牌文具袋各5个共花费120元,购进A品牌文具袋3个和B品牌文具袋4个共花费88元.
(1)求购进A品牌文具袋和B品牌文具袋的单价;
(2)若该文具店购进了A,B两种品牌的文具袋共100个,其中A品牌文具袋售价为12元,B品牌文具袋售价为23元,设购进A品牌文具袋x个,获得总利润为w元.
①求w关于x的函数关系式;
②要使销售文具袋的利润最大,且所获利润不低于进货价格的45%,请你帮该文具店设计一个进货方案,并求出其所获利润的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
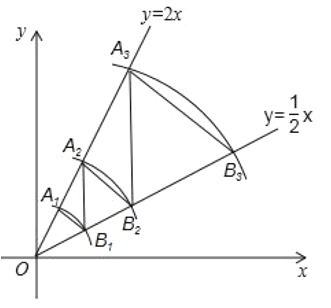
【题目】如图,在平面直角坐标系中,点A1的坐标为(1,2),以点O为圆心,以OA1长为半径画弧,交直线![]() 于点B1.过B1点作B1A2∥y轴,交直线y=2x于点A2,以O为圆心,以OA2长为半径画弧,交直线
于点B1.过B1点作B1A2∥y轴,交直线y=2x于点A2,以O为圆心,以OA2长为半径画弧,交直线![]() 于点B2;过点B2作B2A3∥y轴,交直线y=2x于点A3,以点O为圆心,以OA3长为半径画弧,交直线
于点B2;过点B2作B2A3∥y轴,交直线y=2x于点A3,以点O为圆心,以OA3长为半径画弧,交直线![]() 于点B3;过B3点作B3A4∥y轴,交直线y=2x于点A4,以点O为圆心,以OA4长为半径画弧,交直线
于点B3;过B3点作B3A4∥y轴,交直线y=2x于点A4,以点O为圆心,以OA4长为半径画弧,交直线![]() 于点B4,…按照如此规律进行下去,点B2020的坐标为__________.
于点B4,…按照如此规律进行下去,点B2020的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
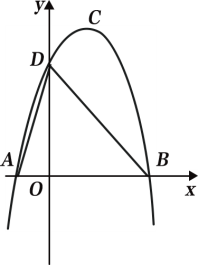
【题目】如图1,抛物线![]() 的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).
的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).
(1)求抛物线的解析式;
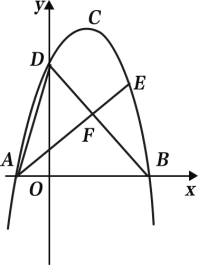
(2)如图2,点E是BD上方抛物线上的一点,连接AE交DB于点F,若AF=2EF,求出点E的坐标.
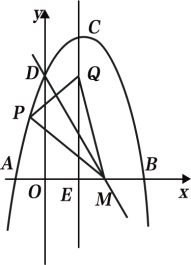
(3)如图3,点M的坐标为(![]() ,0),点P是对称轴左侧抛物线上的一点,连接MP,将MP沿MD折叠,若点P恰好落在抛物线的对称轴CE上,请求出点P的横坐标.
,0),点P是对称轴左侧抛物线上的一点,连接MP,将MP沿MD折叠,若点P恰好落在抛物线的对称轴CE上,请求出点P的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com