
【题目】已知抛物线y=ax2经过点A(2,1).

(1) 求a的值;
(2) 如图1,点M为x轴负半轴上一点,线段AM交抛物线于N.若△OMN为等腰三角形,求点N的坐标;
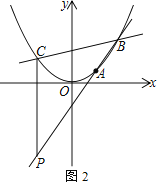
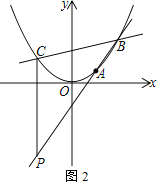
(3) 如图2,直线y=kx-2k+3交抛物线于B、C两点,过点C作CP⊥x轴,交直线AB于点P,请说明点P一定在某条确定的直线上运动,求出这条直线的解析式.
【答案】(1)![]() ;(2)N(﹣1,
;(2)N(﹣1,![]() );(3)y=x﹣3.
);(3)y=x﹣3.
【解析】
(1)A(2,1)代入抛物线方程,解方程即可得到a的值;
(2)设点M(m,0),求出AM所在直线的表达式,MN=ON时,过点N作NH⊥OM,求出OH,HN的长,得出N的坐标,把N点坐标代入抛物线表达式求解即可得出结论;
(3)设:点C(x1,y1),B(x2,y2),P(x1,y),则:![]() x2=kx﹣2k+3,由根与系数的关系得:x1+x2=4k,x1x2=8k﹣12,…①,y2
x2=kx﹣2k+3,由根与系数的关系得:x1+x2=4k,x1x2=8k﹣12,…①,y2![]() ②,把A、B坐标代入直线方程,解得AB所在的直线方程,把点P(x1,y)、①、②代入方程,整理即可得到结论.
②,把A、B坐标代入直线方程,解得AB所在的直线方程,把点P(x1,y)、①、②代入方程,整理即可得到结论.
(1)A(2,1)代入抛物线方程,解得:a![]() ;
;
(2)设点M(m,0),把点A、M坐标代入直线表达式得:
AM所在直线的表达式为:y![]() x
x![]() .
.
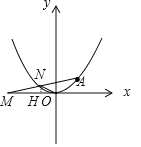
从图象位置关系看,△OMN为等腰三角形时,只有MN=ON这一种情况,过点N作NH⊥OM,则OH=MH![]() ,HN=MHtan∠AMH
,HN=MHtan∠AMH![]() ,则N(
,则N(![]() ,
,![]() ),把N点坐标代入抛物线表达式解得:m=﹣2,m=4(舍去);则N(-1,
),把N点坐标代入抛物线表达式解得:m=﹣2,m=4(舍去);则N(-1,![]() ).
).
经验证:MN=OM,OM=ON无解.故:N(﹣1,![]() );
);
(3)设:点C(x1,y1),B(x2,y2),P(x1,y),则:![]() x2=kx﹣2k+3,则:
x2=kx﹣2k+3,则:![]() ②,把A、B坐标代入直线方程,解得:
②,把A、B坐标代入直线方程,解得:
AB所在的直线方程为:y![]() ,把点P(x1,y)、①、②代入上式,整理得:y=x1﹣3,这条直线的解析式为:y=x﹣3.
,把点P(x1,y)、①、②代入上式,整理得:y=x1﹣3,这条直线的解析式为:y=x﹣3.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中,有![]() 个红球,
个红球,![]() 个白球,这些球除颜色外都相同.
个白球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出![]() 个球,摸到红球的概率是________;
个球,摸到红球的概率是________;
(2)搅匀后先从中任意摸出![]() 个球(不放回),再从余下的球中任意摸出
个球(不放回),再从余下的球中任意摸出![]() 个球.求两次都摸到红球的概率.(用树状图或表格列出所有等可能出现的结果)
个球.求两次都摸到红球的概率.(用树状图或表格列出所有等可能出现的结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
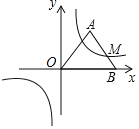
【题目】如图,等腰△OAB的底边OB恰好在x轴上,反比例函数y=![]() 的图象经过AB的中点M,若等腰△OAB的面积为24,则k=( )
的图象经过AB的中点M,若等腰△OAB的面积为24,则k=( )
A. 24B. 18C. 12D. 9
查看答案和解析>>
科目:初中数学 来源: 题型:
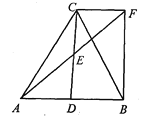
【题目】如图,在△ABC中,D是AB的中点,E是CD的中点, 过点C作CF//AB交AE的延长线于点F,连接BF.
(1) 求证:DB=CF;
(2) 如果AC=BC,试判断四边形BDCF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E是BC的中点,连接DE,过点A作AG⊥ED交DE于点F,交CD于点G.
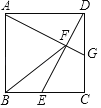
(1)证明:△ADG≌△DCE;(2)连接BF,证明:AB=FB.
查看答案和解析>>
科目:初中数学 来源: 题型:
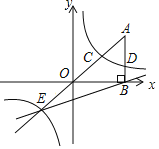
【题目】如图,在平面直角坐标系中,A点的坐标为(a,6),AB⊥x轴于点B,cos∠OAB═![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为
的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为![]() .
.
(1)求反比例函数的解析式;
(2)求直线EB的解析式;
(3)求S△OEB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(6,6),(6,0),抛物线y=﹣(x﹣m)2+n的顶点P在折线OA﹣AB上运动.
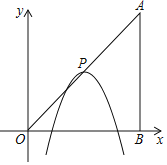
(1)当点P在线段OA上运动时,抛物线y=﹣(x﹣m)2+n与y轴交点坐标为(0,c).
①用含m的代数式表示n,
②求c的取值范围.
(2)当抛物线y=﹣(x﹣m)2+n经过点B时,求抛物线所对应的函数表达式;
(3)当抛物线与△ABO的边有三个公共点时,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
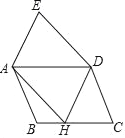
【题目】如图,将平行四边形ABCD绕点D旋转,点C落在BC上的点H处,点B恰好落在点A处,得平行四边形DHAE,若BH=2,CH=3,则DC=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com