
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣![]() 与y轴交于点C,与x轴交于点A(﹣1,0),B(3,0).
与y轴交于点C,与x轴交于点A(﹣1,0),B(3,0).

(1)求这个抛物线的解析式;
(2)将△AOC以每秒一个单位的速度沿x轴向右平移,平移时间为t秒,平移后的△A′O′C′与△BOC重叠部分的面积为S,A与B重合时停止平移,求S与t的函数关系式;
(3)点P在x轴上,连接CP,点B关于直线CP的对称点为B′,若点B′落在这个抛物线的对称轴上,请直接写出所有符合条件的点P的坐标.
【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() ;(2)S=
;(2)S= ;(3)点P的坐标为(
;(3)点P的坐标为(![]() ,0)
,0)
【解析】
(1)将点A,B的坐标代入解析式![]() 即可求得;
即可求得;
(2)分三种情况讨论,设在运动过程中A'C'交OC于点H,交BC于点N,O'C'交BC于点M,分别用含t的代数式表示出相关线段的长度,如图1-1,当0<t≤1时,利用算式S=S梯形O'MCO﹣S△HNC;如图1-2,当1<t≤3时,利用算式S=S△A'BN﹣S△BO'M;如图1-3,当3<t≤4时,利用算式S=S△A'BN,即可以写出结果;
(3)求出抛物线的对称轴,如图2,过C作CG⊥对称轴于点G,利用轴对称的性质及勾股定理求出点B'的坐标,进一步可求出点P的坐标.
(1)将点A(﹣1,0),B(3,0)代入解析式![]() ,
,
得, ,
,
解得,![]() ,
,![]() -
-![]() ,
,
∴抛物线的解析式为:y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() ,
,
(2)在y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 中,当x=0时,y=-
中,当x=0时,y=-![]() ,
,
∴C(0,﹣![]() ),
),
∴在![]() 中,
中,![]() ,
,
∴∠OAC=60°,
在![]() 中,
中,![]() ,
,
∴∠OBC=30°,
设在运动过程中A'C'交OC于点H,交BC于点N,O'C'交BC于点M,
如图1﹣1,当0<t≤1时,

A'O=1﹣t,OH=![]() (1﹣t),HC=OC﹣OH=
(1﹣t),HC=OC﹣OH=![]() t,CN=
t,CN=![]() CH=
CH=![]() t,HN=
t,HN=![]() CN=
CN=![]() t,
t,
BO'=3﹣t,O'M=![]() BO'=
BO'=![]() (3﹣t)=
(3﹣t)=![]() ﹣
﹣![]() t,
t,
∴S=S梯形O'MCO﹣S△HNC
=![]() (
(![]() +
+![]() ﹣
﹣![]() t)t﹣
t)t﹣![]() ×
×![]() t×
t×![]() t
t
=![]() t2+
t2+![]() t;
t;
如图1﹣2,当1<t≤3时,

A'B=4﹣t,A'N=![]() A'B=2﹣
A'B=2﹣![]() t,BN=
t,BN=![]() A'N=2
A'N=2![]() ﹣
﹣![]() t,BO'=3﹣t,MO'=
t,BO'=3﹣t,MO'=![]() BO'=
BO'=![]() ﹣
﹣![]() t,
t,
∴S=S△A'BN﹣S△BO'M
=![]() (2﹣
(2﹣![]() t)(2
t)(2![]() ﹣
﹣![]() t)﹣
t)﹣![]() (3﹣t)(
(3﹣t)(![]() ﹣
﹣![]() t)
t)
=﹣![]() t2+
t2+![]() ;
;
如图1﹣3,当3<t≤4时,

S=S△A'BN
=![]() (2﹣
(2﹣![]() t)(2
t)(2![]() ﹣
﹣![]() t)
t)
=![]() t2﹣
t2﹣![]() t+2
t+2![]() ,
,
综上所述,S= ;
;
(3)在抛物线y=![]() x2﹣
x2﹣![]() x﹣
x﹣![]() 中,
中,
对称轴为x=﹣![]() =1,
=1,
如图2,过C作CG⊥对称轴于点G,

则CG=1,
由轴对称的性质知,CB'=CB=![]() =2
=2![]() ,
,
∴![]() G=
G=![]() =
=![]() ,
,
∴B'(1,![]() ﹣
﹣![]() ),
),
设点P的坐标为(a,0),
由轴对称的性质知,PB=PB',
∴(3﹣a)2=(![]() ﹣
﹣![]() )2+(a﹣1)2,
)2+(a﹣1)2,
解得,a=![]() ,
,
∴点P的坐标为(![]() ,0).
,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长为1,格点△ABC(顶点在网格线的交点上)的顶点A、C的坐标分别为A(﹣3,5)、C(0,3).
(1)请在网格所在的平面内画出平面直角坐标系,并写出点B的坐标.
(2)将△ABC绕着原点顺时针旋转90°得△A1B1C1,画出△A1B1C1.
(3)在直线y=1上存在一点P,使PA+PC的值最小,请直接写出点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系![]() 中的图形M,N,给出如下定义:如果点P为图形M上任意一点,点Q为图形N上任意一点,那么称线段PQ长度的最小值为图形M,N的“近距离”,记作 d(M,N).若图形M,N的“近距离”小于或等于1,则称图形M,N互为“可及图形”.
中的图形M,N,给出如下定义:如果点P为图形M上任意一点,点Q为图形N上任意一点,那么称线段PQ长度的最小值为图形M,N的“近距离”,记作 d(M,N).若图形M,N的“近距离”小于或等于1,则称图形M,N互为“可及图形”.
(1)当⊙O的半径为2时,
①如果点A(0,1),B(3,4),那么d(A,⊙O)=_______,d(B,⊙O)= ________;
②如果直线![]() 与⊙O互为“可及图形”,求b的取值范围;
与⊙O互为“可及图形”,求b的取值范围;
(2)⊙G的圆心G在![]() 轴上,半径为1,直线
轴上,半径为1,直线![]() 与x轴交于点C,与y轴交于点D,如果⊙G和∠CDO互为“可及图形”,直接写出圆心G的横坐标m的取值范围.
与x轴交于点C,与y轴交于点D,如果⊙G和∠CDO互为“可及图形”,直接写出圆心G的横坐标m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
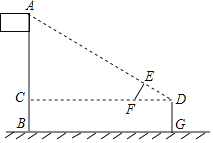
【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=1米,EF=0.5米,测点D到地面的距离DG=3米,到旗杆的水平距离DC=40米,求旗杆的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着交通道路的不断完善,带动了旅游业的发展,某市旅游景区有A、B、C、D、E等著名景点,该市旅游部门统计绘制出2017年“五一”长假期间旅游情况统计图,根据以下信息解答下列问题:

(1)2017年“五一”期间,该市周边景点共接待游客 万人,扇形统计图中A景点所对应的圆心角的度数是 ,并补全条形统计图.
(2)根据近几年到该市旅游人数增长趋势,预计2018年“五一”节将有80万游客选择该市旅游,请估计有多少万人会选择去E景点旅游?
(3)甲、乙两个旅行团在A、B、D三个景点中,同时选择去同一景点的概率是多少?请用画树状图或列表法加以说明,并列举所用等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】y=kx+b的图象经过点(﹣2,2)、(3,7)且与坐标轴相交于点、B两点.
(1)求一次函数的解析式.
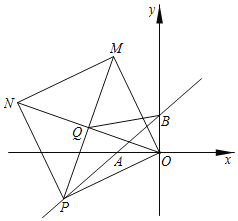
(2)如图,点P是直线AB上一动点,以OP为边作正方形OPNM,连接ON、PM交于点Q,连BQ,当点P在直线AB上运动时,![]() 的值是否会发生变化?若不变,请求出其值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出其值;若变化,请说明理由.
(3)在(2)的条件下,在平面内有一点H,当以H、N、B、P为顶点的四边形为菱形时,直接写出点H的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
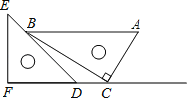
【题目】三角板是我们学习数学的好帮手.将一对直角三角板如图放置,点C在FD的延长线上,点B在ED上,AB∥CF,∠F=∠ACB=90°,∠E=45°,∠A=60°,AC=10,则CD的长度是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
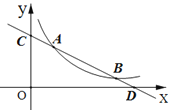
【题目】直线![]() 与反比例函数
与反比例函数![]() (
(![]() >0)的图象分别交于点 A(
>0)的图象分别交于点 A(![]() ,4)和点B(8,
,4)和点B(8,![]() ),与坐标轴分别交于点C和点D.
),与坐标轴分别交于点C和点D.
(1)求直线AB的解析式;
(2)观察图象,当![]() 时,直接写出
时,直接写出![]() 的解集;
的解集;
(3)若点P是![]() 轴上一动点,当△COD与△ADP相似时,求点P的坐标.
轴上一动点,当△COD与△ADP相似时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com