练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在正方形网格中，每个小正方形的边长为1，格点△ABC（顶点在网格线的交点上）的顶点A、C的坐标分别为A（﹣3，5）、C（0，3）．

    （1）请在网格所在的平面内画出平面直角坐标系，并写出点B的坐标．

    （2）将△ABC绕着原点顺时针旋转90°得△A1B1C1，画出△A1B1C1．

    （3）在直线y＝1上存在一点P，使PA+PC的值最小，请直接写出点P的坐标．

    【答案】（1）画图见解析，；（2）答案见解析；（3）答案见解析.

    【解析】

    （1）依据点A、C的坐标分别为A（-3，5）、C（0，3），即可得到平面直角坐标系；
    （2）依据旋转方向、旋转中心以及旋转角度，即可得到△A1B1C1；
    （3）作点C关于直线y=1的对称点'，连接AC'，与直线的交点P即为所求．

    （1）平面直角坐标系如图所示，点B的坐标为(﹣2，1)；

    （2）如图所示，△111即为所求；

    （3）作点C关于直线的对称点'，连接AC'，与直线的交点P即为所求．

    如图所示，点P的坐标为(﹣1，1)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某工程对承接了60万平方米的绿化工程，由于情况有变，……，设原计划每天绿化的面积为万平方米，列方程为，根据方程可知省略的部分是（ ）

    A.实际工作时每天的工作效率比原计划提高了20%，结果提前30天完成了这一任务

    B.实际工作时每天的工作效率比原计划提高了20%，结果延误30天完成了这一任务

    C.实际工作时每天的工作效率比原计划降低了20%，结果延误30天完成了这一任务

    D.实际工作时每天的工作效率比原计划降低了20%，结果提前30天完成了这一任务

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB＝AC，点D为AC中点，点E在BD延长线上，且BD：DE＝3：5，连接CE，tan∠BAC＝，CB＝，则线段EC长为_____．

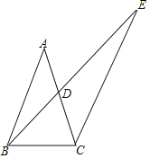
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数y=kx+b（k≠0）的图象与x轴，y轴分别交于A（﹣9，0），B（0，6）两点，过点C（2，0）作直线l与BC垂直，点E在直线l位于x轴上方的部分．

    （1）求一次函数y=kx+b（k≠0）的表达式；

    （2）若△ACE的面积为11，求点E的坐标；

    （3）当∠CBE=∠ABO时，点E的坐标为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝4cm，点P从点A出发以lcm/s的速度沿折线AC﹣CB运动，过点P作PQ⊥AB于点Q，当点P不与点A、B重合时，以线段PQ为边向右作正方形PQRS，设正方形PQRS与△ABC的重叠部分面积为S，点P的运动时间为t（s）．

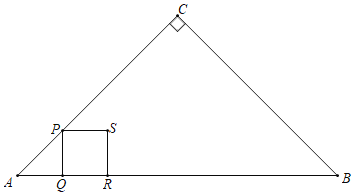
    （1）用含t的代数式表示CP的长度；

    （2）当点S落在BC边上时，求t的值；

    （3）当正方形PQRS与△ABC的重叠部分不是五边形时，求S与t之间的函数关系式；

    （4）连结CS，当直线CS分△ABC两部分的面积比为1：2时，直接写出t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠BAC=90°，将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′，点C的对应点是点C′)，连接CC′，若∠CC′B′=33°，则∠B的大小是(　　)

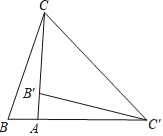
    A. 33° B. 45° C. 57° D. 78°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，△ABC中，AC＝BC，∠ACB＝90°，点P为AB上一点（异于A、B），BD⊥直线CP于D，AE⊥直线CP于E，点F为AB的中点，连接DF．

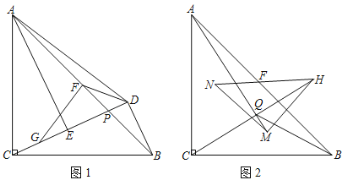
    （1）可以把△ACE绕点F逆时针旋转　 　度（度数不超过180°）和△　 　重合，则∠FDE＝　 　°．

    （2）取CE的中点G，连接AD、FG，求证：AD＝2FG．

    （3）如图2，AB＝8，等腰直角△MNH的斜边NH的中点也为点F，直线AM和直线CH交于点Q，连接BQ，当△MNH绕点F旋转一周时，请直接写出BQ长的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】中华文明，源远流长；中华汉字，寓意深广．为了传承中华民族优秀传统文化，我市某中学举行“汉字听写”比赛，赛后整理参赛学生的成绩，将学生的成绩分为A，B，C，D四个等级，并将结果绘制成如图所示的条形统计图和扇形统计图，但均不完整．

    请你根据统计图解答下列问题：

    （1）参加比赛的学生共有____名；

    （2）在扇形统计图中，m的值为____，表示“D等级”的扇形的圆心角为____度；

    （3）组委会决定从本次比赛获得A等级的学生中，选出2名去参加全市中学生“汉字听写”大赛．已知A等级学生中男生有1名，请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，抛物线y＝ax2+bx﹣与y轴交于点C，与x轴交于点A（﹣1，0），B（3，0）．

    （1）求这个抛物线的解析式；

    （2）将△AOC以每秒一个单位的速度沿x轴向右平移，平移时间为t秒，平移后的△A′O′C′与△BOC重叠部分的面积为S，A与B重合时停止平移，求S与t的函数关系式；

    （3）点P在x轴上，连接CP，点B关于直线CP的对称点为B′，若点B′落在这个抛物线的对称轴上，请直接写出所有符合条件的点P的坐标．

    查看答案和解析>>

    同步练习册答案