Question

【题目】如图，一次函数y=kx+b（k≠0）的图象与x轴，y轴分别交于A（﹣9，0），B（0，6）两点，过点C（2，0）作直线l与BC垂直，点E在直线l位于x轴上方的部分．

（1）求一次函数y=kx+b（k≠0）的表达式；

（2）若△ACE的面积为11，求点E的坐标；

（3）当∠CBE=∠ABO时，点E的坐标为　 　．

Answer 1

【答案】（1）一次函数y=kx+b的表达式为y=x﹣6；（2）E（8，2）；（3）（11，3）．

【解析】

（1）利用待定系数法进行求解即可得；

（2）如图，记直线l与y轴的交点为D，通过证明△OBC∽△OCD，根据相似三角形的性质可求得OD的长，继而可得点D的坐标，再根据点C坐标利用待定系数法求出直线l的解析式为y=x﹣，设E（t，t﹣t），然后根据S△ACE=AC×yE=11，求得t的值即可得解；

（3）如图，过点E作EF⊥x轴于F，可证得△ABO∽△EBC，从而可得，再证明△BOC∽△CFE，可得，从而可得出CF=9，EF=3，继而得到OF=11，即可得点E坐标.

（1）∵一次函数y=kx+b（k≠0）的图象与x轴，y轴分别交于A（﹣9，0），B（0，6）两点，

∴，∴，

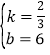∴一次函数y=kx+b的表达式为y=x﹣6；

（2）如图，记直线l与y轴的交点为D，

∵BC⊥l，

∴∠BCD=90°=∠BOC，

∴∠OBC+∠OCB=∠OCD+∠OCB，

∴∠OBC=∠OCD，

∵∠BOC=∠COD，

∴△OBC∽△OCD，

∴，

∵B（0，6），C（2，0），

∴OB=6，OC=2，

∴，

∴OD=，

∴D（0，﹣），

∵C（2，0），

∴直线l的解析式为y=x﹣，

设E（t，t﹣t），

∵A（﹣9，0），C（2，0），

∴S△ACE=AC×yE=×11×（t﹣）=11，

∴t=8，

∴E（8，2）；

（3）如图，过点E作EF⊥x轴于F，

∵∠ABO=∠CBE，∠AOB=∠BCE=90°

∴△ABO∽△EBC，

∴，

∵∠BCE=90°=∠BOC，

∴∠BCO+∠CBO=∠BCO+∠ECF，

∴∠CBO=∠ECF，

∵∠BOC=∠EFC=90°，

∴△BOC∽△CFE，

∴，

∴，

∴CF=9，EF=3，

∴OF=11，

∴E（11，3），

故答案为（11，3）．