
����Ŀ����ͼ����Rt��ABC�У���ACB��90����AC��BC��4cm����P�ӵ�A������lcm/s���ٶ�������AC��CB�˶�������P��PQ��AB�ڵ�Q������P�����A��B�غ�ʱ�����߶�PQΪ��������������PQRS����������PQRS����ABC���ص��������ΪS����P���˶�ʱ��Ϊt��s����
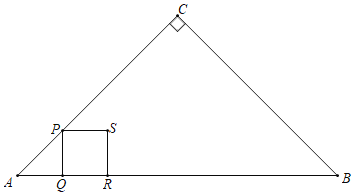
��1���ú�t�Ĵ���ʽ��ʾCP�ij��ȣ�
��2������S����BC����ʱ����t��ֵ��
��3����������PQRS����ABC���ص����ֲ��������ʱ����S��t֮��ĺ�����ϵʽ��
��4������CS����ֱ��CS����ABC�����ֵ������Ϊ1��2ʱ��ֱ��д��t��ֵ��
���𰸡���1����0��t��4ʱ��CP��4��t����4��t��8ʱ��CP��t��4����2��![]() ����3��S��
����3��S��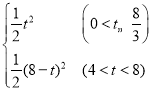 ����4��
����4��![]() ��
��![]()
��������
��1�����������ηֱ���⼴�ɣ�
��2������PA+PC��4���������̼��ɽ�����⣮
��3�����������Σ���ͼ2�У���0��t��![]() ʱ���ص�������������PQRS����4��t��8ʱ���ص������ǡ�PQB���ֱ���⼴�ɣ�
ʱ���ص�������������PQRS����4��t��8ʱ���ص������ǡ�PQB���ֱ���⼴�ɣ�
��4����ֱ��CS��AB��E�����������Σ���ͼ4��1�У���AE��![]() AB��
AB��![]() ʱ��������������ͼ4��2�У���AE��
ʱ��������������ͼ4��2�У���AE��![]() ABʱ�������������ֱ���⼴�ɽ�����⣮
ABʱ�������������ֱ���⼴�ɽ�����⣮
�⣺��1����0��t��4ʱ����AC��4��AP��t��
��PC��AC��AP��4��t��
��4��t��8ʱ��CP��t��4��
��2����ͼ1�У���S����BC���ϣ�
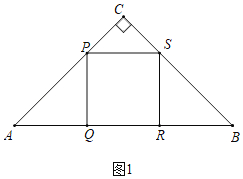
��PA��t��AQ��QP����AQP��90����
��AQ��PQ��PS��![]() t��
t��
��CP��CS����C��90����
��PC��CS��![]() t��
t��
��AP+PC��BC��4��
��t+![]() t��4��
t��4��
���t��![]() ��
��
��3����ͼ2�У���0��t��![]() ʱ���ص�������������PQRS��S����
ʱ���ص�������������PQRS��S����![]() t��2��
t��2��![]() t2��
t2��
��4��t��8ʱ���ص������ǡ�PQB��S��![]() ��8��t��2��
��8��t��2��

����������S��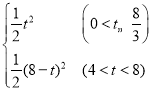 ��
��
��4����ֱ��CS��AB��E��
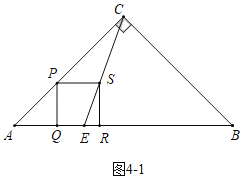
��ͼ4��1�У���AE��![]() AB��
AB��![]() ʱ������������
ʱ������������
��PS��AE��
��![]() ��
��
��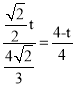 ��
��
���t��![]() ��
��
��ͼ4��2�У���AE��![]() ABʱ������������
ABʱ������������
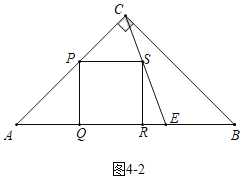
ͬ���ɵã�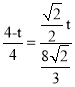 ��
��
���t��![]() ��
��
��������������������t��ֵΪ![]() ��
��![]() ��
��


 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д� �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
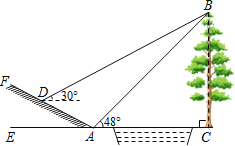
����Ŀ����ͼ��ʾ��ij��ѧ���꼶��ѧ�С��ѡ������ѧУǰ��С�Ӷ�����BC�ĸ߶ȣ�������б����D����ô�������B��������30�㣬����������������6�����µ�A������A����ô�������B��������48�㣮��б��FA���±�i��1��![]() ��������ĸ߶ȣ����������һλС�����ο����ݣ�sin48���0.74��cos48���0.67��tan48���1.11��
��������ĸ߶ȣ����������һλС�����ο����ݣ�sin48���0.74��cos48���0.67��tan48���1.11��![]() ȡ1.73��
ȡ1.73��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����
����![]() ��
��![]() ���ڲ�����
���ڲ�����![]() ��
��![]() ��
��![]() ������������ȣ����
������������ȣ����![]() ��
��![]() �����Ƚǵ������ر�أ����������Ƕ���ȣ����
�����Ƚǵ������ر�أ����������Ƕ���ȣ����![]() ��
��![]() ����ǿ�Ƚǵ���.
����ǿ�Ƚǵ���.
�������
��1������![]() ��
��![]() �ĵȽǵ㣬��
�ĵȽǵ㣬��![]() ����
����![]() �Ķ�����
�Ķ����� ![]() .
.
��2����֪��![]() ��
��![]() ���ⲿ�������
���ⲿ�������![]() ��
��![]() ����࣬������
����࣬������![]() ����
����![]() �����Բ
�����Բ![]() ������
������![]() ����Բ
����Բ![]() �ڵ�
�ڵ�![]() .��
.��![]() �ı��������������ʱ����֤��
�ı��������������ʱ����֤��![]() ��
��![]() �ĵȽǵ�.��Ҫ��ֻѡ������һ�������֤������
�ĵȽǵ�.��Ҫ��ֻѡ������һ�������֤������
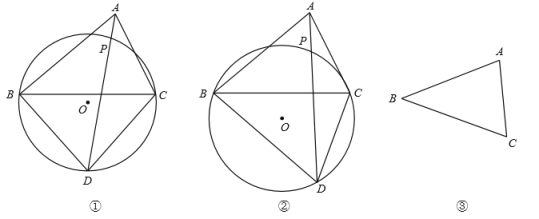
����ͼ�٣�![]()
����ͼ�ڣ�![]()
����˼��
��3����ͼ�ۣ���![]() �У�
��![]() ��
��![]() ��
��![]() ����
��С��![]() ����ֱ�ߺ�Բ��������ǿ�Ƚǵ�
����ֱ�ߺ�Բ��������ǿ�Ƚǵ�![]() .����д������������ͼ�ۼ���
.����д������������ͼ�ۼ���
��4�����й������Ƚǵ�������ǿ�Ƚǵ�����˵����
��ֱ�������ε����������ĵȽǵ㣻
�ڵ��������ε����ĺ����Ķ������ĵȽǵ㣻
���������ε�����������ǿ�Ƚǵ㣻
����һ�������δ���ǿ�Ƚǵ㣬��õ㵽��������������ľ�����ȣ�
����һ�������δ���ǿ�Ƚǵ㣬��õ����������ڲ��������������֮����С�ĵ㣬������ȷ���� .������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ҹ��Ŵ���ѧ�ľ���������������һ�����⣺�����лƽ��ö������һʮһö����֮���ʵȣ�������һ������ʮ�������ʽ���һö���ؼ��Σ�������˼�ǣ��״���װ�лƽ�9ö��ÿö�ƽ�������ͬ�����Ҵ���װ�а���11ö��ÿö����������ͬ��������������ȣ��������ཻ��1ö�״����Ҵ�����13���������������Բ��ƣ����ʻƽ𡢰���ÿö���ض���������ÿö�ƽ���x����ÿö������y������������ã�������
A. ![]()
B. ![]()
C. ![]()
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
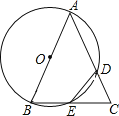
����Ŀ����֪��ABC����ABΪֱ���ġ�O�ֱ�AC��D��BC��E������ED����ED=EC��
��1����֤��AB=AC��
��2����AB=4��BC=![]() ����CD�ij���
����CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������������У�ÿ��С�����εı߳�Ϊ1������ABC�������������ߵĽ����ϣ��Ķ���A��C������ֱ�ΪA����3��5����C��0��3����
��1�������������ڵ�ƽ���ڻ���ƽ��ֱ������ϵ����д����B�����꣮
��2������ABC����ԭ��˳ʱ����ת90��á�A1B1C1��������A1B1C1��
��3����ֱ��y��1�ϴ���һ��P��ʹPA+PC��ֵ��С����ֱ��д����P�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
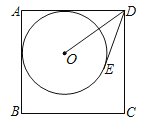
����Ŀ����ͼ����O��������ABCD������AB��AD���У���DE���O�����ڵ�E����AB��7��DO��5����DE�ij���Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
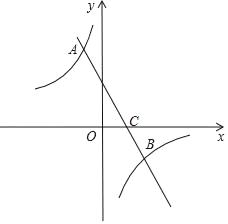
����Ŀ����ͼ��ֱ��y=kx+b��k��0����˫����y=![]() ��m��0�����ڵ�A����
��m��0�����ڵ�A����![]() ��2����B��n����1����
��2����B��n����1����
��1����ֱ����˫���ߵĽ���ʽ��
��2����P��x���ϣ����S��ABP=3�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ž�ͨ��·�IJ������ƣ�����������ҵ�ķ�չ��ij�����ξ�����A��B��C��D��E���������㣬�������β���ͳ�ƻ��Ƴ�2017�ꡰ��һ�������ڼ��������ͳ��ͼ������������Ϣ����������⣺

��1��2017�ꡰ��һ���ڼ䣬�����ܱ߾��㹲�Ӵ��ο� ���ˣ�����ͳ��ͼ��A��������Ӧ��Բ�ĽǵĶ����� ������ȫ����ͳ��ͼ��
��2�����ݽ����굽�������������������ƣ�Ԥ��2018�ꡰ��һ���ڽ���80���ο�ѡ��������Σ�������ж������˻�ѡ��ȥE�������Σ�
��3���ס���������������A��B��D���������У�ͬʱѡ��ȥͬһ����ĸ����Ƕ��٣����û���״ͼ���б�������˵�������о����õȿ��ܵĽ����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com