
ЎѕМвДїЎїДі№¤іМ¶ФіРЅУБЛ60НтЖЅ·ЅГЧµДВМ»Ї№¤іМЈ¬УЙУЪЗйїцУР±дЈ¬ЎЎЈ¬ЙиФјЖ»®ГїМмВМ»ЇµДГж»эОЄ![]() НтЖЅ·ЅГЧЈ¬БР·ЅіМОЄ
НтЖЅ·ЅГЧЈ¬БР·ЅіМОЄ![]() Ј¬ёщѕЭ·ЅіМїЙЦЄКЎВФµДІї·ЦКЗЈЁ Ј©
Ј¬ёщѕЭ·ЅіМїЙЦЄКЎВФµДІї·ЦКЗЈЁ Ј©
A.КµјК№¤ЧчК±ГїМмµД№¤ЧчР§ВК±ИФјЖ»®МбёЯБЛ20%Ј¬Ѕб№ыМбЗ°30МмНкіЙБЛХвТ»ИООс
B.КµјК№¤ЧчК±ГїМмµД№¤ЧчР§ВК±ИФјЖ»®МбёЯБЛ20%Ј¬Ѕб№ыСУОу30МмНкіЙБЛХвТ»ИООс
C.КµјК№¤ЧчК±ГїМмµД№¤ЧчР§ВК±ИФјЖ»®ЅµµНБЛ20%Ј¬Ѕб№ыСУОу30МмНкіЙБЛХвТ»ИООс
D.КµјК№¤ЧчК±ГїМмµД№¤ЧчР§ВК±ИФјЖ»®ЅµµНБЛ20%Ј¬Ѕб№ыМбЗ°30МмНкіЙБЛХвТ»ИООс
Ўѕґр°ёЎїA
ЎѕЅвОцЎї
ёщѕЭ№¤ЧчК±јд=№¤ЧчЧЬБїЎВ№¤ЧчР§ВКЅбєПЛщБР·ЦКЅ·ЅіМЈ¬јґїЙХТіцКЎВФµДМхјюЈ¬ґЛМвµГЅвЈ®
ЅвЈєЙиФјЖ»®ГїМмВМ»ЇµДГж»эОЄxНтЖЅ·ЅГЧЈ¬
ЎЯЛщБР·ЦКЅ·ЅіМКЗ![]() Ј¬
Ј¬
Ўа![]() ОЄКµјК№¤ЧчК±јдЈ¬
ОЄКµјК№¤ЧчК±јдЈ¬![]() ОЄФјЖ»®№¤ЧчК±јдЈ¬
ОЄФјЖ»®№¤ЧчК±јдЈ¬
ЎаКЎВФµДМхјюОЄЈєКµјК№¤ЧчК±ГїМмµД№¤ЧчР§ВК±ИФјЖ»®МбёЯБЛ20%Ј¬Ѕб№ыМбЗ°30МмНкіЙБЛХвТ»ИООс.
№КСЎЈєAЈ®



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїФЪПВБРГьМвЦРЈєЈЁ1Ј©ЕЧОпПЯyЈЅ2ЈЁx©Ѓ3Ј©2©Ѓ6¶ҐµгЧш±кКЗЈЁ3Ј¬©Ѓ6Ј©Ј»ЈЁ2Ј©Т»ФЄ¶юґО·ЅіМx2©Ѓ2x+![]() ЈЅ0µДБЅёщЦ®єНµИУЪ2Ј»ЈЁ3Ј©ТСЦЄЕЧОпПЯyЈЅax2+bx+cЈЁaЈј0Ј©µД¶ФіЖЦбОЄxЈЅ©Ѓ2Ј¬УлxЦбµДТ»ёцЅ»µгОЄЈЁ2Ј¬0Ј©Ј®Иф№ШУЪxµДТ»ФЄ¶юґО·ЅіМax2+bx+cЈЅpЈЁpЈѕ0Ј©УРХыКэёщЈ¬ФтpµДЦµУР4ёцЈ»ЈЁ4Ј©¶юґОєЇКэyЈЅ©Ѓx2©Ѓ2x+cФЪ©Ѓ3ЎЬxЎЬ2µД·¶О§ДЪУРЧоРЎЦµ©Ѓ5Ј¬ФтcµДЦµКЗ©Ѓ2Ј®ЖдЦРХэИ·ЅбВЫµДёцКэКЗЈЁЎЎЎЎЈ©
ЈЅ0µДБЅёщЦ®єНµИУЪ2Ј»ЈЁ3Ј©ТСЦЄЕЧОпПЯyЈЅax2+bx+cЈЁaЈј0Ј©µД¶ФіЖЦбОЄxЈЅ©Ѓ2Ј¬УлxЦбµДТ»ёцЅ»µгОЄЈЁ2Ј¬0Ј©Ј®Иф№ШУЪxµДТ»ФЄ¶юґО·ЅіМax2+bx+cЈЅpЈЁpЈѕ0Ј©УРХыКэёщЈ¬ФтpµДЦµУР4ёцЈ»ЈЁ4Ј©¶юґОєЇКэyЈЅ©Ѓx2©Ѓ2x+cФЪ©Ѓ3ЎЬxЎЬ2µД·¶О§ДЪУРЧоРЎЦµ©Ѓ5Ј¬ФтcµДЦµКЗ©Ѓ2Ј®ЖдЦРХэИ·ЅбВЫµДёцКэКЗЈЁЎЎЎЎЈ©
A.1ёцB.2ёцC.3ёцD.4ёц
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
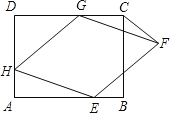
ЎѕМвДїЎїТСЦЄЈ¬ИзНјЈ¬ѕШРОABCDЦРЈ¬ADЈЅ6Ј¬DCЈЅ7Ј¬БвРОEFGHµДИэёц¶ҐµгEЈ¬GЈ¬H·Ц±рФЪѕШРОABCDµД±ЯABЈ¬CDЈ¬DAЙПЈ¬AHЈЅ2Ј¬Б¬ЅУCFЈ®
ЈЁ1Ј©ИфDGЈЅ2Ј¬ЗуЦ¤ЛД±ЯРОEFGHОЄХэ·ЅРОЈ»
ЈЁ2Ј©ИфDGЈЅ6Ј¬ЗуЎчFCGµДГж»эЈ»
ЈЁ3Ј©µ±DGОЄєОЦµК±Ј¬ЎчFCGµДГж»эЧоРЎЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
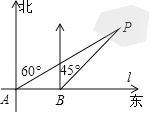
ЎѕМвДїЎїОЄБЛјЖЛгєюЦРРЎµєЙПБ№Н¤PµЅ°¶±Я№«В·lµДѕаАлЈ¬ДіКэС§РЛИ¤РЎЧйФЪ№«В·lЙПµДµгAґ¦Ј¬ІвµГБ№Н¤PФЪ±±Ж«¶«60ЎгµД·ЅПтЙПЈ»ґУAґ¦ПтХэ¶«·ЅПтРРЧЯ200ГЧЈ¬µЅґп№«В·lЙПµДµгBґ¦Ј¬ФЩґОІвµГБ№Н¤PФЪ±±Ж«¶«45ЎгµД·ЅПтЙПЈ¬ИзНјЛщКѕЈ®ЗуБ№Н¤PµЅ№«В·lµДѕаАлЈ®ЈЁЅб№ы±ЈБфХыКэЈ¬ІОїјКэѕЭЈє![]() ЎЦ1.414Ј¬
ЎЦ1.414Ј¬![]() ЎЦ1.732Ј©
ЎЦ1.732Ј©
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
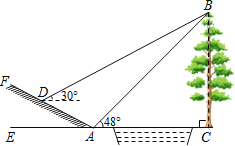
ЎѕМвДїЎїИзНјЛщКѕЈ¬ДіЦРС§ѕЕДкј¶КэС§»о¶ЇРЎЧйСЎ¶ЁІвБїС§РЈЗ°ГжРЎєУ¶Ф°¶ґуКчBCµДёЯ¶ИЈ¬ЛыГЗФЪР±ЖВЙПDґ¦ІвµГґуКч¶Ґ¶ЛBµДСцЅЗКЗ30ЎгЈ¬іЇґуКч·ЅПтПВЖВЧЯ6ГЧµЅґпЖВµЧAґ¦Ј¬ФЪAґ¦ІвµГґуКч¶Ґ¶ЛBµДСцЅЗКЗ48ЎгЈ®ИфР±ЖВFAµДЖВ±ИiЈЅ1Јє![]() Ј¬ЗуґуКчµДёЯ¶ИЈ®ЈЁЅб№ы±ЈБфТ»О»РЎКэЈ©ІОїјКэѕЭЈєsin48ЎгЎЦ0.74Ј¬cos48ЎгЎЦ0.67Ј¬tan48ЎгЎЦ1.11Ј¬
Ј¬ЗуґуКчµДёЯ¶ИЈ®ЈЁЅб№ы±ЈБфТ»О»РЎКэЈ©ІОїјКэѕЭЈєsin48ЎгЎЦ0.74Ј¬cos48ЎгЎЦ0.67Ј¬tan48ЎгЎЦ1.11Ј¬![]() ИЎ1.73Ј®
ИЎ1.73Ј®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
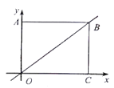
ЎѕМвДїЎїИзНј,ФЪЦ±ЅЗЧш±кПµЦР,ѕШРО![]() µД¶Ґµг
µД¶Ґµг![]() УлЧш±кФµгЦШєП,¶Ґµг
УлЧш±кФµгЦШєП,¶Ґµг![]() ·Ц±рФЪЧш±кЦбµДХэ°лЦбЙП,
·Ц±рФЪЧш±кЦбµДХэ°лЦбЙП, ![]() ,µг
,µг![]() ФЪЦ±ПЯ
ФЪЦ±ПЯ![]() ЙП,Ц±ПЯ
ЙП,Ц±ПЯ![]() УлХЫПЯ
УлХЫПЯ![]() УР№«№Іµг.
УР№«№Іµг.
ЈЁ1Ј©µг![]() µДЧш±кКЗ Ј»
µДЧш±кКЗ Ј»
ЈЁ2Ј©ИфЦ±ПЯ![]() ѕ№эµг
ѕ№эµг![]() Ј¬ЗуЦ±ПЯ
Ј¬ЗуЦ±ПЯ![]() µДЅвОцКЅЈ»
µДЅвОцКЅЈ»
ЈЁ3Ј©¶ФУЪТ»ґОєЇКэ![]() Ј¬µ±
Ј¬µ±![]() Лж
Лж![]() µДФцґу¶шјхРЎК±Ј¬Ц±ЅУРґіц
µДФцґу¶шјхРЎК±Ј¬Ц±ЅУРґіц![]() µДИЎЦµ·¶О§.
µДИЎЦµ·¶О§.
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїЕЧОпПЯy1ЈЅx2+bx+cУлЦ±ПЯy2ЈЅ2x+mПаЅ»УЪAЈЁ1Ј¬4Ј©ЎўBЈЁ©Ѓ1Ј¬nЈ©БЅµгЈ®
ЈЁ1Ј©Зуy1єНy2µДЅвОцКЅЈ»
ЈЁ2Ј©Ц±ЅУРґіцy1©Ѓy2µДЧоРЎЦµЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ЕЧОпПЯ![]() µДНјПу№эµг
µДНјПу№эµг![]() .
.
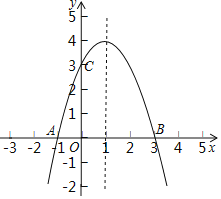
ЈЁ1Ј©ЗуЕЧОпПЯµДЅвОцКЅЈ»
ЈЁ2Ј©ФЪЕЧОпПЯµД¶ФіЖЦбЙПКЗ·сґжФЪТ»µгPЈ¬К№µГЎчPACµДЦЬі¤ЧоРЎЈ¬ИфґжФЪЈ¬ЗлЗуіцµгPµДЧш±кј°ЎчPACµДЦЬі¤Ј»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ»
ЈЁ3Ј©ФЪЈЁ2Ј©µДМхјюПВЈ¬ФЪxЦбЙП·ЅµДЕЧОпПЯЙПКЗ·сґжФЪµгMЈЁІ»УлCµгЦШєПЈ©Ј¬К№µГ![]() ЈїИфґжФЪЈ¬ЗлЗуіцµгMµДЧш±кЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ®
ЈїИфґжФЪЈ¬ЗлЗуіцµгMµДЧш±кЈ»ИфІ»ґжФЪЈ¬ЗлЛµГчАнУЙЈ®
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈє
ЎѕМвДїЎїИзНјЈ¬ФЪХэ·ЅРОНшёсЦРЈ¬ГїёцРЎХэ·ЅРОµД±Яі¤ОЄ1Ј¬ёсµгЎчABCЈЁ¶ҐµгФЪНшёсПЯµДЅ»µгЙПЈ©µД¶ҐµгAЎўCµДЧш±к·Ц±рОЄAЈЁ©Ѓ3Ј¬5Ј©ЎўCЈЁ0Ј¬3Ј©Ј®
ЈЁ1Ј©ЗлФЪНшёсЛщФЪµДЖЅГжДЪ»іцЖЅГжЦ±ЅЗЧш±кПµЈ¬ІўРґіцµгBµДЧш±кЈ®
ЈЁ2Ј©Ѕ«ЎчABCИЖЧЕФµгЛіК±ХлРэЧЄ90ЎгµГЎчA1B1C1Ј¬»іцЎчA1B1C1Ј®
ЈЁ3Ј©ФЪЦ±ПЯyЈЅ1ЙПґжФЪТ»µгPЈ¬К№PA+PCµДЦµЧоРЎЈ¬ЗлЦ±ЅУРґіцµгPµДЧш±кЈ®

Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com