
【题目】y=kx+b的图象经过点(﹣2,2)、(3,7)且与坐标轴相交于点、B两点.
(1)求一次函数的解析式.
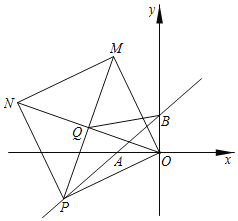
(2)如图,点P是直线AB上一动点,以OP为边作正方形OPNM,连接ON、PM交于点Q,连BQ,当点P在直线AB上运动时,![]() 的值是否会发生变化?若不变,请求出其值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出其值;若变化,请说明理由.
(3)在(2)的条件下,在平面内有一点H,当以H、N、B、P为顶点的四边形为菱形时,直接写出点H的坐标.
【答案】(1)y=x+4;(2)![]() 的值不变,理由见解析;(3) 点H的坐标为
的值不变,理由见解析;(3) 点H的坐标为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)利用待定系数法转化为解方程组解决问题.
(2)如图1中,结论:![]() 的值不变.连接BM,设PB交OM于G.想办法证明∠PBM=90°,利用直角三角形斜边中线的性质以及等腰直角三角形的性质即可解决问题.
的值不变.连接BM,设PB交OM于G.想办法证明∠PBM=90°,利用直角三角形斜边中线的性质以及等腰直角三角形的性质即可解决问题.
(3)分三种情形:如图2﹣1中,当四边形PBNH是菱形时,如图2﹣2中,当点P与A重合时.得到四边形PNMO是正方形(是菱形),此时H与原点O重合.如图2﹣3中,当四边形PBNH是菱形时,分别求解即可解决问题.
解:(1)∵y=kx+b的图象经过点(﹣2,2)、(3,7),
∴![]() ,
,
解得![]() ,
,
∴一次函数的解析式为y=x+4.
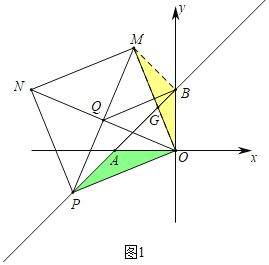
(2)如图1中,结论:![]() 的值不变.
的值不变.
理由:连接BM,设PB交OM于G.
∵直线y=x+4与坐标轴相交于点、B两点,
∴A(﹣4,0),B(0,4),
∴OA=OB=4,
∵四边形POMN是正方形,
∴∠POM=∠AOB=90°,OM=OP,
∴∠AOP=∠BOM,
∵OA=OB,
∴△AOP≌△BOM(SAS),
∴∠OPG=∠GMB,
∵∠OGP=∠BGM,
∴∠GBM=∠GOP=90°,
∴QM=QP,
∴QB=QP=QM,
∵△POQ是等腰直角三角形,
∴OP=![]() QP,
QP,
∴![]() .
.
(3)如图2﹣1中,当四边形PBNH是菱形时,
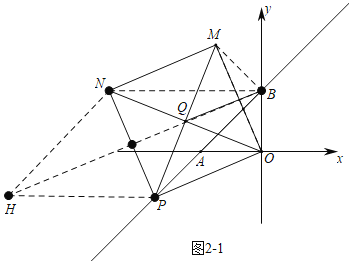
∵BH垂直平分线段PN,BH垂直平分线段OM,
∴BM=OB=4,
∴M(﹣2![]() ,4+2
,4+2![]() ),
),
∴P(﹣4﹣2![]() ,﹣2
,﹣2![]() ),
),
∴BN=BP=![]() ,
,
∴PH=BN=![]() ,
,
∵QB=QN=OQ,
∴∠NBO=90°,
∴BN∥OA∥PH,
∴H(﹣4﹣2![]() ,﹣2
,﹣2![]() ).
).
如图2﹣2中,当点P与A重合时,得到四边形PNMO是正方形(是菱形),此时H与原点O重合,H(0,0).

如图2﹣3中,当四边形PBNH是菱形时,设PH交OB于J,在JO上取一点F,使得PJ=JF.
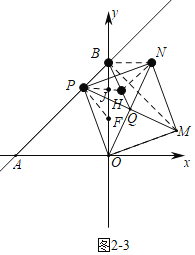
∵BP=BN,
∴∠BPN=∠BNP=22.5°,
∵∠OPN=90°,∠PAO=45°,
∴∠APO=67.5°,
∴∠AOP=67.5°,
∴∠POJ=22.5°,
∵∠PFJ=∠FPO+∠POF=45°,
∴∠FPO=∠POF=22.5°,
∴PF=OF,设PJ=BJ=JF=x,则PB=BN=PF=OF=![]() x,
x,
∴2x+![]() x=4,
x=4,
∴x=4﹣2![]() ,
,
∴BN=PH=4![]() ﹣4,P(2
﹣4,P(2![]() ﹣4,2
﹣4,2![]() ),
),
∴H(6![]() ﹣8,2
﹣8,2![]() ),
),
综上所述,满足条件的点H的坐标为(﹣4﹣2![]() ﹣4
﹣4![]() ,﹣2
,﹣2![]() )或(0,0)或(6
)或(0,0)或(6![]() ﹣8,2
﹣8,2![]() ).
).


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB′C′(点B的对应点是点B′,点C的对应点是点C′),连接CC′,若∠CC′B′=33°,则∠B的大小是( )
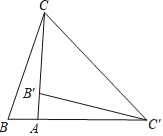
A. 33° B. 45° C. 57° D. 78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 交于点A(2,a).
交于点A(2,a).
(1)求![]() 与
与![]() 的值;
的值;
(2)画出双曲线![]() 的示意图;
的示意图;
(3)设点![]() 是双曲线
是双曲线![]() 上一点(
上一点(![]() 与
与![]() 不重合),直线
不重合),直线![]() 与
与![]() 轴交于点
轴交于点![]() ,当
,当![]() 时,结合图象,直接写出
时,结合图象,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
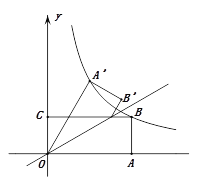
【题目】如图,矩形OABC的边OA,OC分别在![]() 轴、
轴、![]() 轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应),若AB=1,反比例函数
轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应),若AB=1,反比例函数![]() 的图象恰好经过点 A′,B,则
的图象恰好经过点 A′,B,则![]() 的值为_________.
的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣![]() 与y轴交于点C,与x轴交于点A(﹣1,0),B(3,0).
与y轴交于点C,与x轴交于点A(﹣1,0),B(3,0).

(1)求这个抛物线的解析式;
(2)将△AOC以每秒一个单位的速度沿x轴向右平移,平移时间为t秒,平移后的△A′O′C′与△BOC重叠部分的面积为S,A与B重合时停止平移,求S与t的函数关系式;
(3)点P在x轴上,连接CP,点B关于直线CP的对称点为B′,若点B′落在这个抛物线的对称轴上,请直接写出所有符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线![]() 图象的一部分,抛物线的顶点坐标为
图象的一部分,抛物线的顶点坐标为![]() ,与
,与![]() 轴的一个交点为
轴的一个交点为![]() ,点
,点![]() 和点
和点![]() 均在直线
均在直线![]() 上.①
上.①![]() ;②
;②![]() ;③抛物线与
;③抛物线与![]() 轴的另一个交点时
轴的另一个交点时![]() ;④方程
;④方程![]() 有两个不相等的实数根;⑤
有两个不相等的实数根;⑤![]() ;⑥不等式
;⑥不等式![]() 的解集为
的解集为![]() .
.
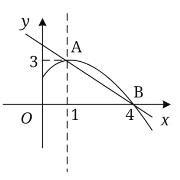
上述六个结论中,其中正确的结论是_____________.(填写序号即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农场今年第一季度的产值为50万元,第二季度由于改进了生产方法,产值提高了![]() ;但在今年第三、第四季度时该农场因管理不善.导致其第四季度的产值与第二季度的产值相比下降了11.4万元.
;但在今年第三、第四季度时该农场因管理不善.导致其第四季度的产值与第二季度的产值相比下降了11.4万元.
(1)求该农场在第二季度的产值;
(2)求该农场在第三、第四季度产值的平均下降的百分率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了满足师生的阅读需求,某校图书馆的藏书从2016年底到2018年底两年内由5万册增加到7.2万册.
(1)求这两年藏书的年均增长率;
(2)经统计知:中外古典名著的册数在2016年底仅占当时藏书总量的5.6%,在这两年新增加的图书中,中外古典名著所占的百分率恰好等于这两年藏书的年均增长率,那么到2018年底中外古典名著的册数占藏书总量的百分之几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店因为换季更新,采购了一批新服装,有A、B两种款式共100件,花费了6600元,已知A种款式单价是80元/件,B种款式的单价是40元/件
(1)求两种款式的服装各采购了多少件?
(2)如果另一个服装店也想要采购这两种款式的服装共60件,且采购服装的费用不超过3300元,那么A种款式的服装最多能采购多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com