
| 2 |
| 3 |
| 6 |
| 2 |
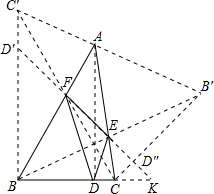 解:根据题意得:当△DEF为△ABC垂足三角形时,周长最小,
解:根据题意得:当△DEF为△ABC垂足三角形时,周长最小,
| ||
| 2 |
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| 6 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 2 | ||
|
| 6 |
| 2 |
| 1 |
| 2 |
| 6 |
| 2 |
| 2 |
| 6 |
| 2 |
| 2 |
| 6 |
| 6 |
| 6 |


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
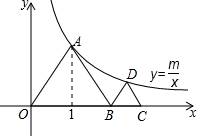 如图,边长为2的等边三角形AOB的顶点在反比例函数y=
如图,边长为2的等边三角形AOB的顶点在反比例函数y=| m |
| x |
A、
| ||||||
B、
| ||||||
C、2
| ||||||
D、2
|
查看答案和解析>>
科目:初中数学 来源: 题型:
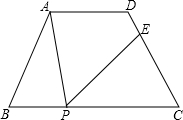 如图,在四边形ABCD中,AD∥BC,∠B=∠C=60°,AD=3,BC=7,P为BC边上的一点(不与B、C重合),过点P作∠APE=∠B,PE交CD于点E.若CE=3,求PE的长.
如图,在四边形ABCD中,AD∥BC,∠B=∠C=60°,AD=3,BC=7,P为BC边上的一点(不与B、C重合),过点P作∠APE=∠B,PE交CD于点E.若CE=3,求PE的长.查看答案和解析>>
科目:初中数学 来源: 题型:
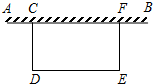 如图,某校广场有一段25米差个的旧围栏,现打算利用该围栏的一部分(或全部)为一边,围成一块100平方米的长方形草坪(如图CDEF,CD<CF)已知整修旧围栏的价格是每米1.75元,建新围栏的价格是4.5元.若CF=x米,计划修建费为y元.
如图,某校广场有一段25米差个的旧围栏,现打算利用该围栏的一部分(或全部)为一边,围成一块100平方米的长方形草坪(如图CDEF,CD<CF)已知整修旧围栏的价格是每米1.75元,建新围栏的价格是4.5元.若CF=x米,计划修建费为y元.查看答案和解析>>
科目:初中数学 来源: 题型:
| 时间x(天) | 1≤x<50 | 50≤x≤90 |
| 售价(元/件) | x+40 | 90 |
| 每天销量(件) | 200-2x | 200-2x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com