
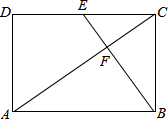
 如图,矩形ABCD中,BE⊥AC于F,E恰是CD的中点,请问BF和AF之间存在怎样的数量关系?并请证明.
如图,矩形ABCD中,BE⊥AC于F,E恰是CD的中点,请问BF和AF之间存在怎样的数量关系?并请证明.| EF•BF |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
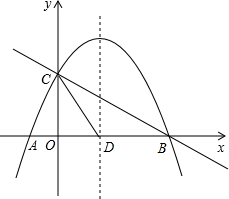 如图,抛物线y=-
如图,抛物线y=-| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
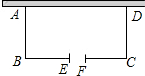 要用防护网围成长方形花坛,其中一面利用现有的一段墙 且在与墙平行的一边开一个2米宽的大门,现有防护栏为91米,花坛面积需要1080米.若墙长50米 求花坛的长和宽?若墙长46米,求长方形的长和宽?墙长对题目有何影响?
要用防护网围成长方形花坛,其中一面利用现有的一段墙 且在与墙平行的一边开一个2米宽的大门,现有防护栏为91米,花坛面积需要1080米.若墙长50米 求花坛的长和宽?若墙长46米,求长方形的长和宽?墙长对题目有何影响?查看答案和解析>>
科目:初中数学 来源: 题型:
| 名称 | 小麦 | 玉米 | 黄豆 |
| 亩产量(千克) | 400 | 600 | 220 |
| 销售单价(元/千克) | 2 | 2 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com