
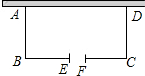
 要用防护网围成长方形花坛,其中一面利用现有的一段墙 且在与墙平行的一边开一个2米宽的大门,现有防护栏为91米,花坛面积需要1080米.若墙长50米 求花坛的长和宽?若墙长46米,求长方形的长和宽?墙长对题目有何影响?
要用防护网围成长方形花坛,其中一面利用现有的一段墙 且在与墙平行的一边开一个2米宽的大门,现有防护栏为91米,花坛面积需要1080米.若墙长50米 求花坛的长和宽?若墙长46米,求长方形的长和宽?墙长对题目有何影响?| 91-(x-2) |
| 2 |
| 91-(x-2) |
| 2 |
| 91-(45-2) |
| 2 |
| 91-(48-2) |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图,在Rt△ABC中,∠ACD=90°,AC=4cm,BC=8cm,点P从点A出发,沿AC以1cm/s的速度向点C匀速运动,同时点Q从点C出发,沿CB以2cm/s的速度向点B匀速运动,连接PQ,设点P的运动时间为t(S)(0<t<4),△CPQ的面积为S(cm2).
如图,在Rt△ABC中,∠ACD=90°,AC=4cm,BC=8cm,点P从点A出发,沿AC以1cm/s的速度向点C匀速运动,同时点Q从点C出发,沿CB以2cm/s的速度向点B匀速运动,连接PQ,设点P的运动时间为t(S)(0<t<4),△CPQ的面积为S(cm2).| 1 |
| 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角坐标系中,以点A(
如图,在直角坐标系中,以点A(| 3 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
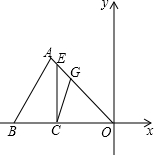 如图,点B、点C都在x轴上,其中点B(-30,0)、C(-20,0),A在第二象限中,△ABO中,∠ABO=45°,∠AOB=30°,过点C作x轴的垂线,与AO交于点E.
如图,点B、点C都在x轴上,其中点B(-30,0)、C(-20,0),A在第二象限中,△ABO中,∠ABO=45°,∠AOB=30°,过点C作x轴的垂线,与AO交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
| a-c |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com