
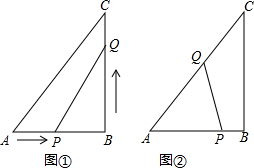
分析 (1)运动所求的时间t,可将BP和BQ的长表示出来,代入三角形面积公式,列出等式,可将时间求出;
(2)设出经t秒,点P移动到AC上,有PB=6-t,AQ=(18-2t)cm,过Q作QD⊥AB,垂足为D,由△AQD∽△ABC得$\frac{QD}{8}$=$\frac{AQ}{AC}$,即QD=$\frac{8(18-2t)}{10}$,代入三角形面积公式,列出等式,可将时间求出.
解答 解:(1)设经过t秒,△PBQ的面积等于5cm2则:
BP=6-t,BQ=2t,
所以S△PBQ=$\frac{1}{2}$×(6-t)×2t=5,
即t2-6t+5=0,
解得:t=1或t=5(不合题意,舍去),
即经过1秒时,△PBQ的面积等于5cm2.
(2)设出经t秒,点P移动到AC上,
则PB=6-t,AQ=(2t-8)cm,
如图②,
过Q作QD⊥AB,垂足为D,
∵△AQD∽△ABC,
∴$\frac{QD}{8}$=$\frac{AQ}{AC}$,
即QD=$\frac{8(18-2t)}{10}$,
$\frac{1}{2}$×(6-t)×$\frac{8(18-2t)}{10}$=5
解得t=$\frac{15±\sqrt{34}}{2}$,
当t=$\frac{15+\sqrt{34}}{2}$时,2t>18,不合题意,舍去;
当t=$\frac{15-\sqrt{34}}{2}$时,符合题意.
所以当△PBQ的面积等于5cm2时t=$\frac{15-\sqrt{34}}{2}$.
点评 本题考查一元二次方程的实际运用,主要是根据三角形的面积公式列出一元二次方程,关键是表示出PB和高的长.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
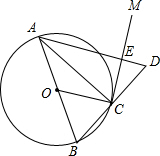 如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线VM,延长BC到D,使BC=CD,连接OC,AD,与CM交于点E.若⊙O的半径为3,ED=2,则△AEC的外接圆的半径为$\sqrt{6}$.
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线VM,延长BC到D,使BC=CD,连接OC,AD,与CM交于点E.若⊙O的半径为3,ED=2,则△AEC的外接圆的半径为$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
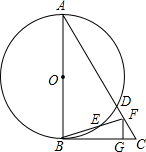 如图,以△ABC边AB为直径的⊙O交AC于点D,点F在DC上,BF交⊙O于点E,BE=EF,∠BAC=2∠CBF,CG⊥BF于点G.
如图,以△ABC边AB为直径的⊙O交AC于点D,点F在DC上,BF交⊙O于点E,BE=EF,∠BAC=2∠CBF,CG⊥BF于点G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com