练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知⊙O的半径为5，弦AB=6，P是AB上任意一点，点C是劣弧的中点，若△POC为直角三角形，则PB的长度（　　）

    A. 1 B. 5 C. 1或5 D. 2或4

    【答案】C

    【解析】

    由点C是劣弧AB的中点，得到OC垂直平分AB，求得DA=DB=3，根据勾股定理得到OD==1，若△POC为直角三角形，只能是∠OPC=90°，则根据相似三角形的性质得到PD=2，于是得到结论．

    ∵点C是劣弧AB的中点，

    ∴OC垂直平分AB，

    ∴DA=DB=3，

    ∴OD=，

    若△POC为直角三角形，只能是∠OPC=90°，

    则△POD∽△CPD，

    ∴，

    ∴PD2=4×1=4，

    ∴PD=2，

    ∴PB=3﹣2=1，

    根据对称性得，

    当P在OC的左侧时，PB=3+2=5，

    ∴PB的长度为1或5.

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

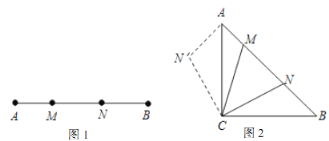
    【题目】定义：如（图1），点把线段分割成和，若以为边的三角形是一个直角三角形，则称点是线段的勾股分割点．

    （1）已知点是线段的勾股分割点，若，求的长；

    （2）如（图2），在等腰直角中， ，点为边上两点，满足，求证：点是线段的勾股分割点；阳阳同学在解决第（2）小题时遇到了困难，陈老师对阳阳说：要证明勾股分割点，则需设法构造直角三角形，你可以把绕点逆时针旋转试一试．请根据陈老师的提示完成第（2）小题的证明过程．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知∠1＝∠2，要使△ABD≌△ACD，需从下列条件中增加一个，错误的选法是（ ）

    A.∠ADB＝∠ADCB.∠B＝∠CC.AB＝ACD.DB＝DC

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】A、B两种机器人都被用来搬运化工原料，A型机器人比B型机器人每小时多搬运30kg，A型机器人搬运900kg与B型机器人搬运600kg所用时间相等，两种机器人每小时分别搬运多少化工原料？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

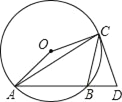
    【题目】如图，点A、B、C均在⊙O上，过点C作⊙O的切线交AB的延长线于点D，∠ACB=45°，∠AOC=150°．

    （1）求证：CD=CB；

    （2）⊙O的半径为，求AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE．求证：

    （1）△AEF≌△CEB；

    （2）AF=2CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC和△DCE中，CA=CB，CD=CE，∠CAB= ∠CED=α.

    (1)如图1，将AD、EB延长，延长线相交于点0.

    ①求证:BE= AD;

    ②用含α的式子表示∠AOB的度数(直接写出结果);

    (2)如图2,当α=45°时，连接BD、AE,作CM⊥AE于M点，延长MC与BD交于点N.求证:N是BD的中点.

    注:第(2)问的解答过程无需注明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

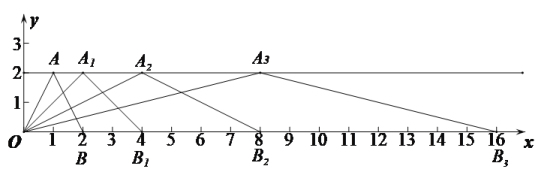
    【题目】如下图所示，在直角坐标系中，第一次将△OAB变换成，第二次将变换成，第三次将变换成，已知，，，，，，．

    （1）观察每次变换前后的三角形有何变化，找出规律，按此规律再将变换成，则的坐标为 ，的坐标为 ．

    （2）可以发现变换过程中……的纵坐标均为 ．

    （3）按照上述规律将△OAB进行n次变换得到，则可知的坐标为 ， 的坐标为 ．

    （4）线段的长度为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某居民小区为了绿化小区环境，建设和谐家园，准备将一块周长为76米的长方形空地，设计成长和宽分别相等的9块小长方形，如图所示，计划在空地上种上各种花卉，经市场预测，绿化每平方米空地造价210元，请计算，要完成这块绿化工程，预计花费多少元？

    查看答案和解析>>

    同步练习册答案