
【题目】已知坐标平面上的机器人接受指令“[a , A]”(a≥0,0°<A<180°)后的行动结果为:在原地顺时针旋转A后,再向面对方向沿直线行走a.若机器人的位置在原点,面对方向为y轴的负半轴,则它完成一次指令[2,60°]后,所在位置的坐标为( )
A.(-1, ![]() )
)
B.(-1, ![]() )
)
C.( ![]() ,-1)
,-1)
D.( ![]() ,-1)
,-1)
【答案】D
【解析】设机器人现在的位置为点A,那么OA=2,作AB⊥y轴于B,作AC⊥x轴于C,那么AC=1,AB= ![]() ,所以机器人所在位置的坐标为(
,所以机器人所在位置的坐标为( ![]() ,-1).
,-1).
【考点精析】通过灵活运用坐标与图形变化-对称和解直角三角形,掌握关于x轴对称的点的特征:两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x轴的对称点为P’(x,-y);关于y轴对称的点的特征:两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于y轴的对称点为P’(-x,y);解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,∠AOB内一点P,P1 , P2分别是P关于OA、OB的对称点,P1P2交OA于点M,交OB于点N.若△PMN的周长是5cm,则P1P2的长为( ) 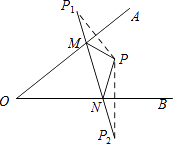
A.3cm
B.4cm
C.5cm
D.6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,如果把图中任一条线段沿方格线平移1格称为“1步”,那么要通过平移使图中的3条线段首尾相接组成一个三角形,最少需要
A.4步
B.5步
C.6步
D.7步
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=x2先向左平移1个单位,再向下平移2个单位得到的抛物线是( )
A.y=(x+1)2﹣2
B.y=(x﹣1)2+2
C.y=(x﹣1)2﹣2
D.y=(x+1)2+2
查看答案和解析>>
科目:初中数学 来源: 题型:
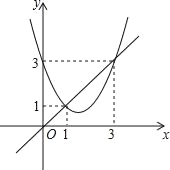
【题目】函数y=x2+bx+c与y=x的图象如图所示,有以下结论:
①b2﹣4c>0;②b+c+1=0;③3b+c+6=0;④当1<x<3时,x2+(b﹣1)x+c<0.
其中正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系,请你从所得到的关系中任选一个加以说明.(适当添加辅助线,其实并不难)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com