
【题目】如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是( ) 
A.18 ![]() ﹣9π
﹣9π
B.18﹣3π
C.9 ![]() ﹣
﹣ ![]()
D.18 ![]() ﹣3π
﹣3π
【答案】A
【解析】解:∵四边形ABCD是菱形,∠DAB=60°, ∴AD=AB=6,∠ADC=180°﹣60°=120°,
∵DF是菱形的高,
∴DF⊥AB,
∴DF=ADsin60°=6× ![]() =3
=3 ![]() ,
,
∴图中阴影部分的面积=菱形ABCD的面积﹣扇形DEFG的面积=6×3 ![]() ﹣
﹣ ![]() =18
=18 ![]() ﹣9π.
﹣9π.
故选:A.
【考点精析】利用菱形的性质和扇形面积计算公式对题目进行判断即可得到答案,需要熟知菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,将边长为2cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,若两个三角形重叠部分的面积为1cm2 , 则它移动的距离AA′等于( ) 
A.0.5cm
B.1cm
C.1.5cm
D.2cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图为人民公园中的荷花池,现要测量此荷花池两旁A、B两棵树间的距离(我们不能直接量得).请你根据所学知识,以卷尺和测角仪为测量工具设计一种测量方案.
要求:(1)画出你设计的测量平面图;
(2)简述测量方法,并写出测量的数据(长度用![]() …表示;角度用
…表示;角度用![]() …表示);
…表示);
(3)根据你测量的数据,计算A、B两棵树间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
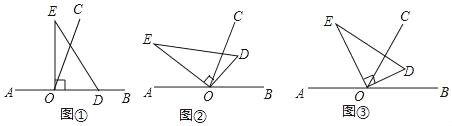
【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OC恰好平分∠BOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O转动,如果OD始终在∠BOC的内部,试猜想∠BOD和∠COE有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由同样大小的正方形按照一定规律所组成的,其中第①个图形中一个有2个正方形,第②个图形中一共有8个正方形,第③个图形中一共有16个正方形,…,按此规律,第⑦个图形中正方形的个数为( )

A. 56 B. 65 C. 68 D. 71
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)计算:﹣22+| ![]() ﹣4|+(
﹣4|+( ![]() )﹣1+2tan60°.
)﹣1+2tan60°.
(2)先化简,再求值:( ![]() ﹣
﹣ ![]() )÷
)÷ ![]() ,其中x是不等式3x+7>1的负整数解.
,其中x是不等式3x+7>1的负整数解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的个数是( )
(1)﹣a表示负数;
(2)多项式﹣3a2b+7a2b2﹣2ab+l的次数是3;
(3)单项式﹣![]() 的系数为﹣2;
的系数为﹣2;
(4)一个有理数不是整数就是分数
A. 0个 B. 1个 C. 2个 D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小丽化简的过程,仔细阅读后解答所提出的问题.
解:a(a+2b)﹣(a﹣1)2﹣2a
=a2+2ab﹣a2﹣2a﹣1﹣2a 第一步
=2ab﹣4a﹣1.第二步
(1)小丽的化简过程从第 步开始出现错误;
(2)请对原整式进行化简,并求当a=![]() ,b=﹣6时原整式的值.
,b=﹣6时原整式的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解青少年形体情况,现随机抽查了某市若干名初中学生坐姿、站姿、走姿的好坏情况.我们对测评数据作了适当处理(如果一个学生有一种以上不良姿势,以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请你根据图中所给信息解答下列问题: 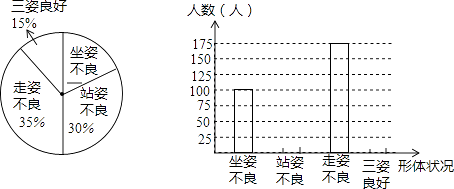
(1)请将两幅统计图补充完整;
(2)请问这次被抽查形体测评的学生一共是多少人?
(3)如果全市有5万名初中生,那么全市初中生中,坐姿和站姿不良的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com