
 如图,在平面直角坐标系中,Rt△ABC的顶点B在原点0,直角边BC在x轴的正半轴上,∠ACB=90°,点A的坐标为(3,$\sqrt{3}$).点D是BC边上一个动点(不与点B,C重合),过点D作DE⊥BC交AB边于点E,将∠ABC沿直线DE翻折,点B落在x轴上的点F处.若△AEF为直角三角形.求点F的坐标.
如图,在平面直角坐标系中,Rt△ABC的顶点B在原点0,直角边BC在x轴的正半轴上,∠ACB=90°,点A的坐标为(3,$\sqrt{3}$).点D是BC边上一个动点(不与点B,C重合),过点D作DE⊥BC交AB边于点E,将∠ABC沿直线DE翻折,点B落在x轴上的点F处.若△AEF为直角三角形.求点F的坐标. 分析 根据直角三角形的定义可分三种情况考虑:①当∠AEF=90°时,通过角的计算得出∠OED=45°=60°,自相矛盾,故此种情况不存在;②当∠AEF=90°时,根据角的计算得出∠FAC=30°,结合A点的坐标利用∠FAC的正切值可求出CF的长,再由边与边的关系即可得出OF的长,从而得出F点的坐标;③当∠EAF=90°时,根据角的计算得出∠CAF=30°,结合A点的坐标利用∠CAF的正切值可求出CF的,再由边与边的关系即可得出OF的长,从而得出F点的坐标.综合以上3种情况即可得出结论.
解答 解:△AEF为直角三角形分三种情况:
①当∠AEF=90°时,
∵∠OED=∠FED,且∠OED+∠FED+∠AEF=180°,
∴∠OED=45°.
∵∠ACB=90°,点A的坐标为(3,$\sqrt{3}$),
∴tan∠ABC=$\frac{\sqrt{3}}{3}$,∠ABC=30°.
∵ED⊥x轴,
∴∠OED=90°-∠ABC=60°.
45°≠60°,此种情况不可能出现;
②当∠AFE=90°时,
∵∠OED=∠FED=60°,
∴∠AEF=60°,
∵∠AFE=90°,
∴∠EAF=90°-∠AEF=30°.
∵∠BAC=90°-∠ABC=60°,
∴∠FAC=∠BAC-∠EAF=60°-30°=30°.
∵AC=$\sqrt{3}$,
∴CF=AC•tan∠FAC=1,
∴OF=OC-FC=3-1=2.
即此时点F的坐标为(2,0);
③当∠EAF=90°时,
∵∠BAC=60°,
∴∠CAF=∠EAF-∠EAC=90°-60°=30°,
∵AC=$\sqrt{3}$,
∴CF=AC•tan∠FAC=1,
∴OF=OC+CF=3+1=4.
即此时点F的坐标为(4,0).
综上知:若△AEF为直角三角形.点F的坐标为(2,0)、(4,0).
点评 本题考查了一次函数图象与几何变换、角的计算以及解直角三角形,解题的关键是根据角的计算以及解直角三角形找出CF的长度.本题属于中档题,难度不大,但在解决该类题型时,部分同学往往会落掉2种情况,只得出F点的坐标为(2,0),因此在平常教学中应多加对学生引导,培养他们考虑问题的全面性.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
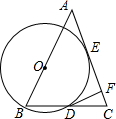 如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1.
如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 若实数a,b在数轴上的位置如图所示,则$\frac{b+1}{a+1}+\frac{b}{a}$的结果是( )
若实数a,b在数轴上的位置如图所示,则$\frac{b+1}{a+1}+\frac{b}{a}$的结果是( )| A. | 正数 | B. | 零 | C. | 负数 | D. | 非正数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
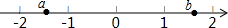 实数a,b在数轴上的位置如图,且a=-$\sqrt{2}$,b=$\sqrt{3}$,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-|a-b|的结果为( )
实数a,b在数轴上的位置如图,且a=-$\sqrt{2}$,b=$\sqrt{3}$,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$-|a-b|的结果为( )| A. | -2$\sqrt{2}$ | B. | -2$\sqrt{3}$ | C. | 0 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
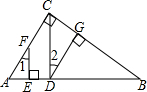 已知,如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2.试判断CD与AB的位置关系,并说明理由.请完成下列解答:
已知,如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2.试判断CD与AB的位置关系,并说明理由.请完成下列解答:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com