
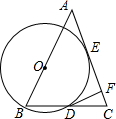
 如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1.
如图,△ABC中,AB=AC,O为AB上一点,以O为圆心,OB为半径的⊙O与AC切于点E,与BC交于点D,过D作⊙O的切线交AC于F,⊙O的半径为3,CF=1.分析 (1)连接OD、OE,由切线的性质得出∠OEF=∠ODF=90°,由等腰三角形的性质得出∠ODB=∠C,证出OD∥AC,得出AC⊥DF,因此∠EFD=90°,证出四边形ODFE是矩形,由OD=OE,证出四边形ODFE是正方形,得出OE=DF=EF=OD=OB=3,由勾股定理求出CD即可;
(2)设AB=AC=x,则OA=x-3,AE=x-4,在Rt△AOE中,由勾股定理得出方程,解方程即可.
解答 解:(1)连接OD、OE,如图所示: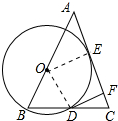
∵OB为半径的⊙O与AC切于点E,DF是⊙O的切线,
∴OE⊥AC,OD⊥DF,
∴∠OEF=∠ODF=90°,
∵AB=AC,
∴∠B=∠C,
∵OB=OD,
∴∠B=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∴AC⊥DF,
∴∠EFD=90°,
∴四边形ODFE是矩形,
又∵OD=OE,
∴四边形ODFE是正方形,
∴OE=DF=EF=OD=OB=3,
∵∠DFC=90°,
∴CD=$\sqrt{D{F}^{2}+C{F}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$;
(2)设AB=AC=x,则OA=x-3,AE=x-4,
在Rt△AOE中,AE2+OE2=OA2,
即(x-4)2+32=(x-3)2,
解得:x=8,
即AB的长为8.
点评 本题考查了切线的性质、等腰三角形的性质、平行线的判定、正方形的判定与性质、勾股定理等知识;本题综合性强,有一定难度,证明四边形ODFE是正方形是解决问题的关键.


科目:初中数学 来源:2016-2017学年浙江省杭州市萧山区戴村片八年级3月月考数学试卷(解析版) 题型:解答题
如果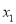 ,
, 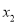 是一元二次方程
是一元二次方程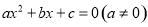 的两根,那么
的两根,那么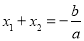 ,
, 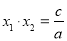 ,这就是著名的韦达定理.
,这就是著名的韦达定理.
已知m,n是方程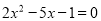 的两根,不解方程计算:
的两根,不解方程计算:
(1) 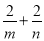 ;
;
(2) 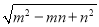 .
.
查看答案和解析>>
科目:初中数学 来源:2017届湖北省大冶市九年级3月中考模拟数学试卷(解析版) 题型:单选题
下列运算正确的是( )
A. 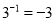 B.
B. 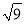 = ±3 C. (ab2)3= a3b6 D. a6÷a2 = a3
= ±3 C. (ab2)3= a3b6 D. a6÷a2 = a3
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
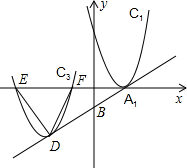 如图,抛物线C1:y=(x-2)2,直线l:y=$\frac{1}{2}$x-1,顶点为A1,l与y轴交于B点,将C1沿A1B方向平移n个单位的C3,且C3的顶点及x轴的两个交点为顶点的三角形为正三角形,求n.
如图,抛物线C1:y=(x-2)2,直线l:y=$\frac{1}{2}$x-1,顶点为A1,l与y轴交于B点,将C1沿A1B方向平移n个单位的C3,且C3的顶点及x轴的两个交点为顶点的三角形为正三角形,求n.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
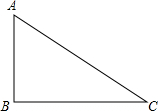 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,Rt△ABC的顶点B在原点0,直角边BC在x轴的正半轴上,∠ACB=90°,点A的坐标为(3,$\sqrt{3}$).点D是BC边上一个动点(不与点B,C重合),过点D作DE⊥BC交AB边于点E,将∠ABC沿直线DE翻折,点B落在x轴上的点F处.若△AEF为直角三角形.求点F的坐标.
如图,在平面直角坐标系中,Rt△ABC的顶点B在原点0,直角边BC在x轴的正半轴上,∠ACB=90°,点A的坐标为(3,$\sqrt{3}$).点D是BC边上一个动点(不与点B,C重合),过点D作DE⊥BC交AB边于点E,将∠ABC沿直线DE翻折,点B落在x轴上的点F处.若△AEF为直角三角形.求点F的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
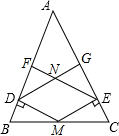 已知:如图,M是等腰三角形ABC的底边BC的中点,MD⊥AB,ME⊥AC,EF⊥AB,DG⊥AC,垂足分别为为D,E,F,G,DG与EF交于点N,求证:四边形DMEN是菱形.
已知:如图,M是等腰三角形ABC的底边BC的中点,MD⊥AB,ME⊥AC,EF⊥AB,DG⊥AC,垂足分别为为D,E,F,G,DG与EF交于点N,求证:四边形DMEN是菱形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com