
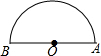
 如图所示,在半圆O中,AB为直径,P为弧AB的中点,分别在弧AP和弧PB上取中点A1和B1,再在弧PA1和弧PB1上分别取中点A2和B2,若一直这样取中点,求∠AnPBn=180°-$\frac{1}{{2}^{n+1}}$×180°.
如图所示,在半圆O中,AB为直径,P为弧AB的中点,分别在弧AP和弧PB上取中点A1和B1,再在弧PA1和弧PB1上分别取中点A2和B2,若一直这样取中点,求∠AnPBn=180°-$\frac{1}{{2}^{n+1}}$×180°. 分析 根据已知条件AB为⊙O直径,P为弧AB的中点,弧AP和弧PB上取中点A1和B1,得到∠A1OB1=$\frac{1}{2}$∠AOB=$\frac{1}{2}×$180°,根据圆周角定理和圆内接四边形的性质得到∠A1PB1=180°-$\frac{1}{2}∠$A1OB1=180°-$\frac{1}{2}×\frac{1}{2}$×180°=180°-$\frac{1}{{2}^{2}}$×180,进一步得到∠A2PB2=180°-$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×$180°=180°-$\frac{1}{{2}^{3}}$×180°,即可得到结论.
解答 解:∵AB为⊙O直径,P为弧AB的中点,弧AP和弧PB上取中点A1和B1,
∴∠A1OB1=$\frac{1}{2}$∠AOB=$\frac{1}{2}×$180°,
∴∠A1PB1=180°-$\frac{1}{2}∠$A1OB1=180°-$\frac{1}{2}×\frac{1}{2}$×180°=180°-$\frac{1}{{2}^{2}}$×180,
∴∠A2PB2=180°-$\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×$180°=180°-$\frac{1}{{2}^{3}}$×180°,
…
∴∠AnPBn=180°-$\frac{1}{{2}^{n+1}}$×180°,
故答案为:180°-$\frac{1}{{2}^{n+1}}$×180°.
点评 本题考查了圆周角定理,圆内接四边形的性质,找准规律是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
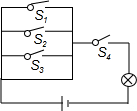 如图所示,是物理课上李老师让小刘同学连接的电路图,现要求:随机同时闭合开关S1、S2、S3、S4中的两个算一次操作,则小刘同学操作一次就能使灯泡?发光的概率是( )
如图所示,是物理课上李老师让小刘同学连接的电路图,现要求:随机同时闭合开关S1、S2、S3、S4中的两个算一次操作,则小刘同学操作一次就能使灯泡?发光的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 1 | 2 | 3 | 4 | … |
| 2 | 4 | 6 | 8 | … |
| 3 | 6 | 9 | 12 | … |
| 4 | 8 | 12 | 16 | … |
| … | … | … | … | … |
| 15 | |
| 24 | |
| a |
| 16 | |
| 24 | |
| b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com