
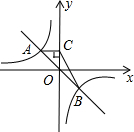
 如图.函数y=-kx(k>0)与y=-$\frac{4}{x}$的图象交于A、B两点,过点A作AC垂直于y轴于点C,求△ABC的面积.
如图.函数y=-kx(k>0)与y=-$\frac{4}{x}$的图象交于A、B两点,过点A作AC垂直于y轴于点C,求△ABC的面积.  口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
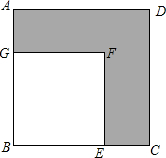 如图,工人张师傅要在一块大正方形ABCD中切下一块小的正方形BEFG,若阴影部分面积为240mm2,AB=2x+8,BE=2x-4,求大正方形的边长.
如图,工人张师傅要在一块大正方形ABCD中切下一块小的正方形BEFG,若阴影部分面积为240mm2,AB=2x+8,BE=2x-4,求大正方形的边长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
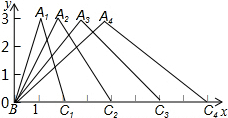 小新制作了很多等腰三角形,把它们都放在平面直角坐标系中,使点B与原点重合,底边在x轴的正半轴上.
小新制作了很多等腰三角形,把它们都放在平面直角坐标系中,使点B与原点重合,底边在x轴的正半轴上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
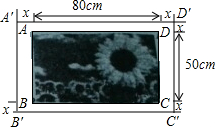 如图,在一幅长为80cm,宽为50cm的矩形画ABCD的四周镶一条金色纸边,制成一幅矩形挂图A′B′C′D′.如果金色镶边纸的宽度x为5cm,那么原风景画ABCD与矩形挂图A′B′C′D′是否相似?并说明理由.
如图,在一幅长为80cm,宽为50cm的矩形画ABCD的四周镶一条金色纸边,制成一幅矩形挂图A′B′C′D′.如果金色镶边纸的宽度x为5cm,那么原风景画ABCD与矩形挂图A′B′C′D′是否相似?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com