
【题目】仿照例题完成任务:
例:如图1,在网格中,小正方形的边长均为![]() ,点
,点![]() ,
,![]() ,
,![]() ,
,![]() 都在格点上,
都在格点上,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
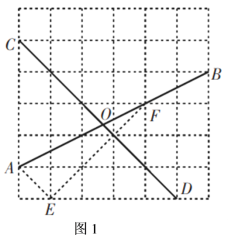
解析:连接![]() ,
,![]() ,导出
,导出![]() ,再根据勾股定理求得三角形各边长,然后利用三角函数解决问题.具体解法如下:
,再根据勾股定理求得三角形各边长,然后利用三角函数解决问题.具体解法如下:
连接![]() ,
,![]() ,则
,则![]() ,
,
![]() ,根据勾股定理可得:
,根据勾股定理可得:
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() 是直角三角形,
是直角三角形,![]() ,
,
![]()
即![]() .
.
任务:
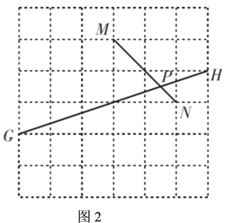
(1)如图2,![]() ,
,![]() ,
,![]() ,
,![]() 四点均在边长为
四点均在边长为![]() 的正方形网格的格点上,线段
的正方形网格的格点上,线段![]() ,
,![]() 相交于点
相交于点![]() ,求图中
,求图中![]() 的正切值;
的正切值;
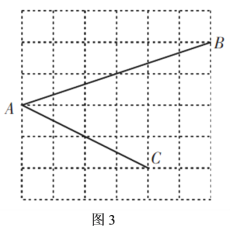
(2)如图3,![]() ,
,![]() ,
,![]() 均在边长为
均在边长为![]() 的正方形网格的格点上,请你直接写出
的正方形网格的格点上,请你直接写出![]() 的值.
的值.
科目:初中数学 来源: 题型:
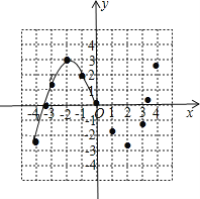
【题目】某学习小组在研究函数![]() 的图象与性质时,已列表、描点并画出了图象的一部分.
的图象与性质时,已列表、描点并画出了图象的一部分.

(1)请补全函数图象;
(2)方程![]() 实数根的个数为______;
实数根的个数为______;
(3)观察图象,写出该函数的两条性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
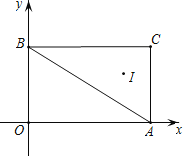
【题目】如图,在平面直角坐标系xOy中,A(4,0),B(0,3),C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I'的坐标为( )
A. (﹣2,3) B. (﹣3,2) C. (3,﹣2) D. (2,﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
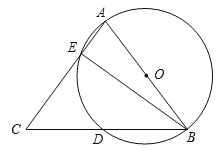
【题目】如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且点D为![]() 的中点.
的中点.
(1)若∠A=70°,求∠DBE的度数;
(2)求证:AB=AC;
(3)若⊙O的半径为5cm,BC=12cm,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E,D,连接EC,CD.
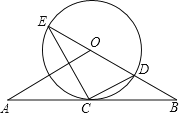
(1)求证:直线AB是⊙O的切线;
(2)若tan∠CED=![]() ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教练想从甲、乙两名运动员中选拔一人参加射击锦标赛,故先在射击队举行了一场选拔比赛.在相同的条件下各射靶![]() 次,每次射靶的成绩情况如图所示.
次,每次射靶的成绩情况如图所示.
甲射靶成绩的条形统计图
| 乙射靶成绩的折线统计图
|
(![]() )请你根据图中的数据填写下表:
)请你根据图中的数据填写下表:
平均数 | 众数 | 方差 | |
甲 | __________ |
|
|
乙 |
| __________ | __________ |
(![]() )根据选拔赛结果,教练选择了甲运动员参加射击锦标赛,请给出解释.
)根据选拔赛结果,教练选择了甲运动员参加射击锦标赛,请给出解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读资料:我们把顶点在圆上,并且一边和圆相交、另一边和圆相切的角叫做弦切角,如下左图∠ABC所示。
同学们研究发现:P为圆上任意一点,当弦AC经过圆心O时,且AB切⊙O于点A,此时弦切角∠CAB=∠P(图甲)
证明:∵AB切⊙O于点A, ∴∠CAB=90°, 又∵AC是直径, ∴∠P=90° ∴∠CAB=∠P
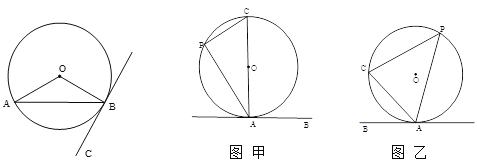
问题拓展:若AC不经过圆心O(如图乙),该结论:弦切角∠CAB=∠P还成立吗?
请说明理由。
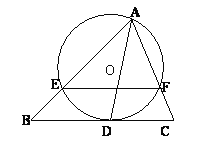
知识运用:如图,AD是△ABC中∠BAC的平分线,经过点A的⊙O与BC切于点D,与AB、AC分别相交于E、F。 求证:EF∥BC。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).
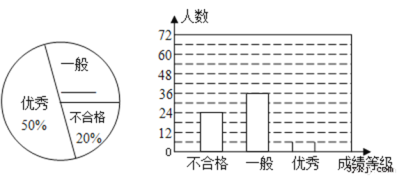
请你根据图中所给的信息解答下列问题:
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有 人达标;
(3)若该校学生有1200人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com