
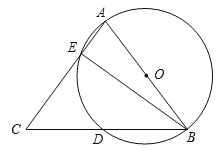
【题目】如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且点D为![]() 的中点.
的中点.
(1)若∠A=70°,求∠DBE的度数;
(2)求证:AB=AC;
(3)若⊙O的半径为5cm,BC=12cm,求线段BE的长.
【答案】(1)35°;(2)详见解析;(3)![]() .
.
【解析】
(1)点D为![]() 的中点,则OD⊥BE,且BH=HE,∠ODB=∠OBD=
的中点,则OD⊥BE,且BH=HE,∠ODB=∠OBD=![]() (180°﹣70°)=55°,∠OBE=90°﹣70°=20°,即可求解;
(180°﹣70°)=55°,∠OBE=90°﹣70°=20°,即可求解;
(2)由(1)得:OD是△ABC的中位线,则OD=![]() AC=
AC=![]() AB,即可求解;
AB,即可求解;
(3)△ABC为等腰三角形,则cosC=![]() =cos∠ODB,则sin∠ODB=
=cos∠ODB,则sin∠ODB=![]() ,BE=2BH=2BDsin∠ODB,即可求解.
,BE=2BH=2BDsin∠ODB,即可求解.
(1)连接OD交BE于点H,连接AD,
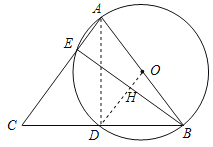
∵点D为![]() 的中点,则OD⊥BE,且BH=HE,
的中点,则OD⊥BE,且BH=HE,
AB为直径,则∠AEB=90°,∴OD∥AC,且OD是△ABC的中位线,
∵∠CAB=70°,则∠DOB=70°,∠ODB=∠OBD=![]() (180°﹣70°)=55°
(180°﹣70°)=55°
∠OBE=90°﹣70°=20°,
则∠DBE=∠OBD﹣∠OBE=55°﹣20°=35°;
(2)由(1)得:OD是△ABC的中位线,则OD=![]() AC=
AC=![]() AB,
AB,
故AB=AC;
(3)△ABC为等腰三角形,则cosC=![]() =cos∠ODB,则sin∠ODB=
=cos∠ODB,则sin∠ODB=![]() ,
,
BE=2BH=2BDsin∠ODB=2×6×![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图1,2).请根据统计图解答下列问题:
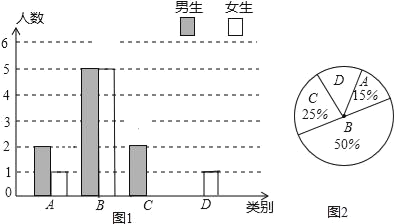
(1)本次调查中,王老师一共调查了 名学生;
(2)将条形统计图补充完整;
(3)为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,点D是AB边上的一点,连结CD,过点C作CD的垂线,与经过点C、D、B的圆交于点E,连结DE,交CB于点F.若AD=1,DB=3,则线段DE的长为_____;△CDF的面积为_____.
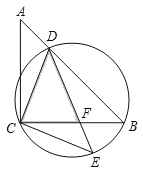
查看答案和解析>>
科目:初中数学 来源: 题型:
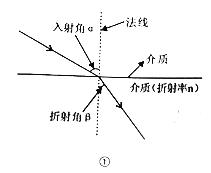
【题目】光线从空气射入水中会发生折射现象,发生折射时,满足的折射定律如图①所示:折射率![]() (
(![]() 代表入射角,
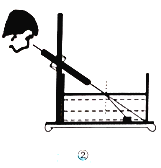
代表入射角,![]() 代表折射角).小明为了观察光线的折射现象,设计了图②所示的实验;通过细管可以看见水底的物块,但从细管穿过的直铁丝,却碰不上物块,图③是实验的示意图,点A,C,B在同一直线上,测得
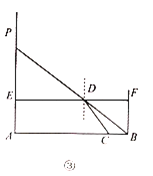
代表折射角).小明为了观察光线的折射现象,设计了图②所示的实验;通过细管可以看见水底的物块,但从细管穿过的直铁丝,却碰不上物块,图③是实验的示意图,点A,C,B在同一直线上,测得![]() ,则光线从空射入水中的折射率n等于________.
,则光线从空射入水中的折射率n等于________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仿照例题完成任务:
例:如图1,在网格中,小正方形的边长均为![]() ,点
,点![]() ,
,![]() ,
,![]() ,
,![]() 都在格点上,
都在格点上,![]() 与
与![]() 相交于点
相交于点![]() ,求
,求![]() 的值.
的值.
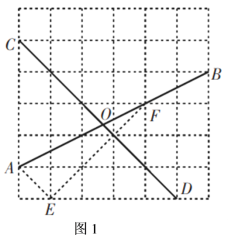
解析:连接![]() ,
,![]() ,导出
,导出![]() ,再根据勾股定理求得三角形各边长,然后利用三角函数解决问题.具体解法如下:
,再根据勾股定理求得三角形各边长,然后利用三角函数解决问题.具体解法如下:
连接![]() ,
,![]() ,则
,则![]() ,
,
![]() ,根据勾股定理可得:
,根据勾股定理可得:
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() 是直角三角形,
是直角三角形,![]() ,
,
![]()
即![]() .
.
任务:
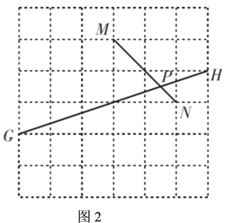
(1)如图2,![]() ,
,![]() ,
,![]() ,
,![]() 四点均在边长为
四点均在边长为![]() 的正方形网格的格点上,线段
的正方形网格的格点上,线段![]() ,
,![]() 相交于点
相交于点![]() ,求图中
,求图中![]() 的正切值;
的正切值;
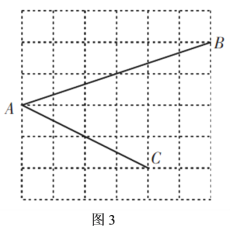
(2)如图3,![]() ,
,![]() ,
,![]() 均在边长为
均在边长为![]() 的正方形网格的格点上,请你直接写出
的正方形网格的格点上,请你直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
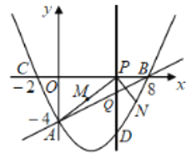
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 过点
过点![]() ,动点P在线段
,动点P在线段![]() 上以每秒2个单位长度的速度由点
上以每秒2个单位长度的速度由点![]() 运动到点
运动到点![]() 停止,设运动时间为
停止,设运动时间为![]() ,过点
,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() , 交抛物线于点
, 交抛物线于点![]() .连接
.连接![]() ,
,![]() 是线段
是线段![]() 的中点,将线段
的中点,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得线段
得线段![]() .
.
(1)求抛物线的解析式;
(2)连接![]() ,当
,当![]() 为何值时,
为何值时,![]() 面积有最大值,最大值是多少?
面积有最大值,最大值是多少?
(3)当![]() 为何值时,点
为何值时,点![]() 落在抛物线上.
落在抛物线上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com