
【题目】2016年4月23日是我国第一个“全民阅读日”某校开展了“建设书香校园,捐赠有益图书”活动.我们在参加活动的所有班级中,随机抽取了一个班,已知这个班是八年级5班,全班共50名学生.现将该班捐赠图书情况的统计结果,绘制成如下两幅不完整的统计图.
请你根据以上信息,解答下列问题:
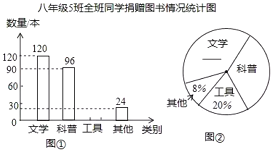
(1)补全上面的条形统计图和扇形统计图;
(2)求八年级5班平均每人捐赠了多少本书?
(3)若该校八年级共有800名学生,请你估算这个年级学生共可捐赠多少本书?
【答案】(1)见解析;(2)6本书;(3)4800本书
【解析】
(1)观察两统计图可知全班捐赠图书的总数=其它书的数量÷其它书的数量所占的百分比,列式计算;再利用全班捐赠图书的总数×捐赠工具类书的数量所占的百分比,就可求出捐赠工具类书的数量,就可补全条形统计图;然后利用部分的数量÷总数,就可求出文学类和科普类所占的百分比,从而可以补全扇形统计图中的数据;
(2)用全班捐赠图书的总数除以八年级5班的人数,列式计算;
(3)用800×平均每一个人的捐赠图书的数量,列式计算.
(1)解:全班捐赠图书的总数为24÷8%=300(本),
则捐赠工具类书有300×20%=60(本),
文学类百分比为![]() ×100%=40%,
×100%=40%,
科普类百分比为![]() ×100%=32%,
×100%=32%,
完成统计图如下:
八年级5班全班同学捐赠图书情况统计图

(2)解:八年级5班平均每人捐赠了![]() =6本书;
=6本书;
(3)解:∵800×6=4800,
估算这个年级学生共可捐赠4800本书.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:初中数学 来源: 题型:
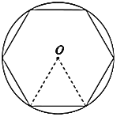
【题目】中国魏晋时期的数学家刘徽首创“割圆术”,奠定了中国圆周率计算在世界上的领先地位.刘徽提出:“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣”,由此求得圆周率![]() 的近似值.如图,设半径为
的近似值.如图,设半径为![]() 的圆内接正
的圆内接正![]() 边形的周长为
边形的周长为![]() ,圆的直径为
,圆的直径为![]() ,当
,当![]() 时,
时,![]() ,则当
,则当![]() 时,
时,![]() ______.(结果精确到0.01,参考数据:
______.(结果精确到0.01,参考数据:![]() ,
,![]()
![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
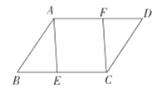
【题目】八年级6班的一个互助学习小组组长收集并整理了组员们讨论如下问题时所需的条件.如图所示,在四边形![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,____________________.求证:四边形
上,____________________.求证:四边形![]() 是平行四边形.你能在横线上填上最少且简捷的条件使结论成立吗?条件分别是:①
是平行四边形.你能在横线上填上最少且简捷的条件使结论成立吗?条件分别是:①![]() ;②
;②![]() ;③
;③![]() ;④四边形
;④四边形![]() 是平行四边形,其中A、B、C、D四位同学所填条件符合题目要求的是( )
是平行四边形,其中A、B、C、D四位同学所填条件符合题目要求的是( )
A.①②B.①②③C.①④D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形![]() 中,
中,![]() 在
在![]() 上从
上从![]() 向
向![]() 运动,连接
运动,连接![]() 交
交![]() 于
于![]() 连接
连接![]() .
.
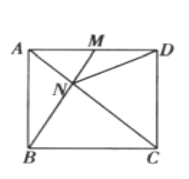
(1)证明:无论![]() 运动到
运动到![]() 上的何处,都有
上的何处,都有![]() ;
;
(2)当![]() 运动到何处时,
运动到何处时,![]() ?
?
(3)若![]() 从
从![]() 到
到![]() 再从
再从![]() 到
到![]() ,在整个运动过程中,
,在整个运动过程中,![]() 为多少时,
为多少时,![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,△AOB是等腰直角三角形,∠AOB=90°,点A(2,1).
(1)求点B的坐标;
(2)求经过A、O、B三点的抛物线的函数表达式;
(3)在(2)所求的抛物线上,是否存在一点P,使四边形ABOP的面积最大?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文具店有三种品牌的6个笔记本,价格是4,5,7(单位:元)三种,从中随机拿出一个本,已知![]() (一次拿到7元本)
(一次拿到7元本)![]() .
.
(1)求这6个本价格的众数.
(2)若琪琪已拿走一个7元本,嘉嘉准备从剩余5个本中随机拿一个本.
①所剩的5个本价格的中位数与原来6个本价格的中位数是否相同?并简要说明理由;
②嘉嘉先随机拿出一个本后不放回,之后又随机从剩余的本中拿一个本,用列表法求嘉嘉两次都拿到7元本的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
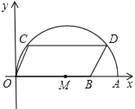
【题目】如图,在平面直角坐标系中,点A的坐标是(10,0),点B的坐标为(8,0),点C,D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,![]() ),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值_____.
),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com