
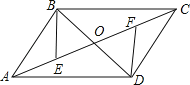
【题目】如图,ABCD的对角线AC、BD相交于点O,AE=CF.
(1) 求证:△BOE≌△DOF;
(2) 连接DE、BF,若BD⊥EF,试探究四边形EBDF的形状,并对结论给予证明.
【答案】(1)见解析;(2)四边形EBDF为菱形,理由见解析
【解析】
(1)根据平行四边形的性质可得BO=DO,AO=CO,再利用等式的性质可得EO=FO,然后再利用SAS定理判定△BOE≌△DOF即可;
(2)根据BO=DO,FO=EO可得四边形BEDF是平行四边形,再根据对角线互相垂直的平行四边形是菱形可得四边形EBDF为菱形.
证明:(1) ∵四边形ABCD是平行四边形,
∴BO=DO,AO=CO,
∵AE=CF,
∴AO﹣AE=CO﹣FO,
∴EO=FO,
在△BOE和△DOF中
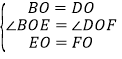 ,
,
∴△BOE≌△DOF(SAS);
(2) 四边形EBDF为菱形,等三角形的判定,以及菱形的判定,关键是掌握
理由:∵BO=DO,FO=EO,
∴四边形BEDF是平行四边形,
∵BD⊥EF,
∴四边形EBDF为菱形.


科目:初中数学 来源: 题型:
【题目】综合题
(1)如图1,△ABC中,∠BAC=90°,AB=AC,AE是过A点的一条直线,且B、C在AE的异侧,BD⊥AE于D,CE⊥AE于E,求证:BD=DE+CE.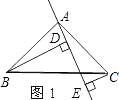
(2)若直线AE绕点A旋转到图2的位置时(BD<CE),其余条件不变,问BD与DE、CE的关系如何?请予以证明.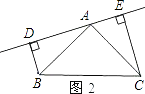
查看答案和解析>>
科目:初中数学 来源: 题型:
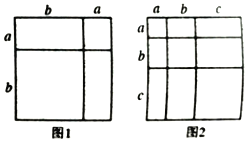
【题目】对于一个图形通过两种不同的方法计算它的面积,可以得到一个数学等式,例如图1可以得到![]() ,请解答下列问题:
,请解答下列问题:
(1)写出图2中所表示的数学等式;
(2)根据整式乘法的运算法则,通过计算验证上述等a式;
(3)若a+b+c=l0,ab+ac+bc=35,利用得到的结论,求.![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线a:y=2x﹣6,和直线b:y=﹣ ![]() x+4相交于点H,分别与x、y轴交于点A、B、C、D,点P在x轴上,过点P作x轴的垂线,分别与直线a、b交于点E、F.
x+4相交于点H,分别与x、y轴交于点A、B、C、D,点P在x轴上,过点P作x轴的垂线,分别与直线a、b交于点E、F.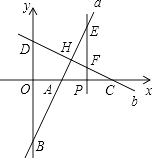
(1)求点H的坐标;
(2)判断直线a、b的位置关系,并说明理由;
(3)设点P的横坐标为m,当m为何值时,以D、E、F、O为顶点的四边形是
平行四边形,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
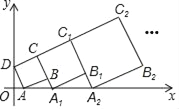
【题目】在平面直角坐标系中,正方形ABCD的位置如右图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2017个正方形的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况、他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图.

分组 | 频数 | 百分比 |
600≤x<800 | 2 | 5% |
800≤x<1000 | 6 | 15% |
1000≤x<1200 | 45% | |
9 | 22.5% | |
1600≤x<1800 | 2 | |
合计 | 40 | 100% |
根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市路桥公司决定对A、B两地之间的公路进行改造,并由甲工程队从A地向B地方向修筑,乙工程队从B地向A地方向修筑.已知甲工程队先施工2天,乙工程队再开始施工,乙工程队施工几天后因另有任务提前离开,余下的任务由甲工程队单独完成,直到公路修通.甲、乙两个工程队修公路的长度y(米)与施工时间x(天)之间的函数关系如图所示.下列说法:①乙工程队每天修公路240米;②甲工程队每天修公路120米;③甲比乙多工作6天;④A、B两地之间的公路总长是1680米.其中正确的说法有( )
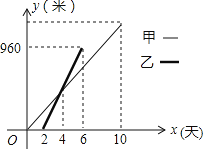
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com