
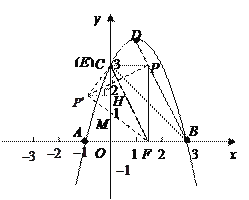
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=ax2+bx+c(aЁй0)ОЙ§AЃЈ-1ЃЌ0ЃЉЃЌBЃЈ3ЃЌ0ЃЉЃЌCЃЈ0ЃЌ3ЃЉШ§ЕуЃЌЦфЖЅЕуЮЊDЃЌСЌНгBDЃЌЕуЪЧЯпЖЮBDЩЯвЛИіЖЏЕуЃЈВЛгыBЁЂDжиКЯЃЉЃЌЙ§ЕуPзїyжсЕФДЙЯпЃЌДЙзуЮЊEЃЌСЌНгBEЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЌВЂаДГіЖЅЕуDЕФзјБъЃЛ
ЃЈ2ЃЉШчЙћPЕуЕФзјБъЮЊЃЈxЃЌyЃЉЃЌЁїPBEЕФУцЛ§ЮЊЃЌЧѓSгыxЕФКЏЪ§ЙиЯЕЪНЃЌаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЌВЂЧѓГіSЕФзюДѓжЕЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕБSШЁЕУзюДѓжЕЪБЃЌЙ§ЕуPзїxЕФДЙЯпЃЌДЙзуЮЊFЃЌСЌНгEFЃЌАбЁїPEFбижБЯпEFелЕўЃЌЕуPЕФЖдгІЕуЮЊPЁфЃЌЧыжБНгаДГіPЁфЕузјБъЃЌВЂХаЖЯЕуPЁфЪЧЗёдкИУХзЮяЯпЩЯЃЎ

ЁОД№АИЁПЃЈ1ЃЉЖЅЕуDЕФзјБъЮЊ(1ЃЌ4)ЃЛЃЈ2ЃЉЕБ![]() ЪБЃЌ SШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ
ЪБЃЌ SШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ![]() ЃЛЃЈ3ЃЉАбPЁфзјБъЃЈ
ЃЛЃЈ3ЃЉАбPЁфзјБъЃЈ![]() ЃЉДњШыХзЮяЯпНтЮіЪНЃЌВЛГЩСЂЃЌЫљвд
ЃЉДњШыХзЮяЯпНтЮіЪНЃЌВЛГЩСЂЃЌЫљвд![]() ВЛдкХзЮяЯпЩЯЃЎ
ВЛдкХзЮяЯпЩЯЃЎ
ЁОНтЮіЁП
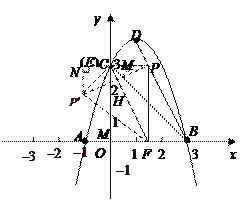
ЃЈ1ЃЉИљОнAЃЌBЃЌCШ§ЕуЕФзјБъЃЌПЩвддЫгУНЛЕуЪНЗЈЧѓЕУХзЮяЯпЕФНтЮіЪНЃЎдйИљОнЖЅЕуЕФзјБъЙЋЪНЧѓЕУХзЮяЯпЕФЖЅЕузјБъЃЛ
ЃЈ2ЃЉИљОнBЃЌDЕФзјБъдЫгУД§ЖЈЯЕЪ§ЗЈЧѓЕУжБЯпBDЕФНтЮіЪНЃЌдйИљОнШ§НЧаЮЕФУцЛ§ЙЋЪНвдМАyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЕУЕНsгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎЕуPЕФКсзјБъМДxЕФжЕЮЛгкЕуDКЭЕуBЕФКсзјБъжЎМфЃЎИљОнЖўДЮКЏЪ§ЕФЖЅЕуЪНМДПЩЗжЮіЦфзюжЕЃЛ
ЃЈ3ЃЉИљОнЃЈ2ЃЉжаЕФзјБъЕУЕуEКЭЕуCжиКЯЃЎЙ§PЁфзїPЁфHЁЭyжсгкHЃЌPЁфFНЛyжсгкЕуMЃЎвЊЧѓPЁфHКЭOHЕФГЄЃЎPЁфHЕФГЄПЩвддЫгУжБНЧШ§НЧаЮPЁфCMЕФУцЛ§НјааМЦЫуЃЎЩшMCЃНmЃЌдђMFЃНmЃЌPЁфMЃН3mЃЌPЁфEЃН32ЃЎИљОнЙДЙЩЖЈРэСаЗНГЬЧѓНтЃЌЕУЕНжБНЧШ§НЧаЮPЁфCMЕФШ§БпКѓЃЌдйИљОнжБНЧШ§НЧаЮЕФУцЛ§ЙЋЪННјааМЦЫуЃЎвЊЧѓOHЕФГЄЃЌвбжЊЕуCЕФзјБъЃЌжЛашИљОнЙДЙЩЖЈРэНјвЛВНЧѓЕУCHЕФГЄМДПЩЃЎАбЧѓЕУЕФЕуPЕФзјБъДњШыХзЮяЯпНтЮіЪНМДПЩХаЖЯЕуPЁфЪЧЗёдкИУХзЮяЯпЩЯЃЎ
ЃЈ1ЃЉЩш![]() ЃЌ
ЃЌ
Аб![]() ДњШыЃЌЕУ
ДњШыЃЌЕУ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
ЖЅЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЩшжБЯп![]() НтЮіЪНЮЊЃК
НтЮіЪНЮЊЃК![]() ЃЈ
ЃЈ![]() ЃЉЃЌАб
ЃЉЃЌАб![]() СНЕузјБъДњШыЃЌ
СНЕузјБъДњШыЃЌ
ЕУ![]()
НтЕУ![]() ЃЌ
ЃЌ
ЁржБЯп![]() НтЮіЪНЮЊ
НтЮіЪНЮЊ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ
ШЁЕУзюДѓжЕЃЌзюДѓжЕЮЊ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЕБ![]() ШЁЕУзюДѓжЕЃЌ
ШЁЕУзюДѓжЕЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЫФБпаЮ![]() ЪЧОиаЮЃЌ
ЪЧОиаЮЃЌ
зїЕу![]() ЙигкжБЯп
ЙигкжБЯп![]() ЕФЖдГЦЕу
ЕФЖдГЦЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ
ЗЈвЛЃКЙ§![]() зї
зї![]() жсгк
жсгк![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌ
ЃЌ
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
дк![]() жаЃЌгЩЙДЙЩЖЈРэЃЌ
жаЃЌгЩЙДЙЩЖЈРэЃЌ
![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
гЩ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() зјБъ
зјБъ![]() ЃЛ
ЃЛ
ЗЈЖўЃКСЌНг![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌЗжБ№Й§Еу
ЃЌЗжБ№Й§Еу![]() зї
зї![]() ЕФДЙЯпЃЌДЙзуЮЊ
ЕФДЙЯпЃЌДЙзуЮЊ![]() ЃЌ
ЃЌ
взжЄ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
гЩШ§НЧаЮжаЮЛЯпЖЈРэЃЌ
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Ёр![]() зјБъ
зјБъ![]() ЃЎ
ЃЎ
Аб![]() зјБъ
зјБъ![]() ДњШыХзЮяЯпНтЮіЪНЃЌВЛГЩСЂЃЌЫљвд
ДњШыХзЮяЯпНтЮіЪНЃЌВЛГЩСЂЃЌЫљвд![]() ВЛдкХзЮяЯпЩЯЃЎ
ВЛдкХзЮяЯпЩЯЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЁїABCКЭЁїDBEОљЮЊЕШбќжБНЧШ§НЧаЮЃЎ
ЃЈ1ЃЉЧѓжЄЃКAD=CEЃЛ
ЃЈ2ЃЉЧѓжЄЃКADКЭCEДЙжБЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌEЮЊACЕФжаЕуЃЌADЦНЗжЁЯBACЃЌBAЃКCA=2ЃК3ЃЌADгыBEЯрНЛгкЕуOЃЌШєЁїOAEЕФУцЛ§БШЁїBODЕФУцЛ§Дѓ1ЃЌдђЁїABCЕФУцЛ§ЪЧЃЈЁЁЁЁЃЉ

A. 8 B. 9 C. 10 D. 11
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,ADЪЧRtЁїABCаББпBCЩЯЕФИп.
ЃЈ1ЃЉГпЙцзїЭМ:зїЁЯCЕФЦНЗжЯп,НЛABгкЕуE,НЛADгкЕуFЃЈВЛаДзїЗЈ,БиаыБЃСєзїЭМКлМЃ,БъЩЯгІгаЕФзжФИЃЉ;
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТ,Й§FЛBCЕФЦНааЯпНЛACгкЕуH,ЯпЖЮFHгыЯпЖЮCHЕФЪ§СПЙиЯЕШчКЮ?ЧыгшвджЄУї;
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТ,СЌНсDEDH.ЧѓжЄ:EDЁЭHD.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНЭЌбЇжЛгавЛеХЦЙХвЧђБШШќЕФУХЦБЃЌЫЖМЯыШЅЃЌзюКѓЩЬЖЈЭЈЙ§зЊХЬгЮЯЗОіЖЈЃЎгЮЯЗЙцдђЪЧЃКзЊЖЏЯТУцЦНОљЗжГЩШ§ИіЩШаЮЧвБъгаВЛЭЌбеЩЋЕФзЊХЬЃЌзЊХЬСЌајзЊЖЏСНДЮЃЌШєжИеыЧАКѓЫљжИбеЩЋЯрЭЌЃЌдђМзШЅЃЛЗёдђввШЅЃЎЃЈШчЙћжИеыЧЁКУЭЃдкЗжИюЯпЩЯЃЌФЧУДжизЊвЛДЮЃЌжБЕНжИеыжИЯђвЛжжбеЩЋЮЊжЙЃЉ

ЃЈ1ЃЉзЊХЬСЌајзЊЖЏСНДЮЃЌжИеыЫљжИбеЩЋЙВгаМИжжЧщПіЃПЭЈЙ§ЛЪїзДЭМЛђСаБэЗЈМгвдЫЕУїЃЛ
ЃЈ2ЃЉФуШЯЮЊетИігЮЯЗЙЋЦНТ№ЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
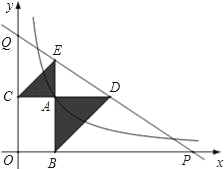
ЁОЬтФПЁПШчЭМЃЌвбжЊЖЏЕуAдкКЏЪ§y=![]() ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЃЌABЁЭxжсгкЕуBЃЌACЁЭyжсгкЕуCЃЌбгГЄCAжСЕуDЃЌЪЙAD=ABЃЌбгГЄBAжСЕуEЃЌЪЙAE=ACЃЌжБЯпDEЗжБ№НЛxжсЃЌyжсгкЕуPЃЌQЃЌЕБQEЃКDP=9ЃК25ЪБЃЌЭМжаЕФвѕгАВПЗжЕФУцЛ§ЕШгк___ЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓЩЯЃЌABЁЭxжсгкЕуBЃЌACЁЭyжсгкЕуCЃЌбгГЄCAжСЕуDЃЌЪЙAD=ABЃЌбгГЄBAжСЕуEЃЌЪЙAE=ACЃЌжБЯпDEЗжБ№НЛxжсЃЌyжсгкЕуPЃЌQЃЌЕБQEЃКDP=9ЃК25ЪБЃЌЭМжаЕФвѕгАВПЗжЕФУцЛ§ЕШгк___ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжБНЧзјБъЯЕжаЃЌвбжЊAЃЈ1ЃЌ0ЃЉЃЌвдЕуAЮЊдВаФЛдВЃЌЕуMЃЈ4ЃЌ4ЃЉдкЁбAЩЯЃЌжБЯпy=Љ![]() x+bЙ§ЕуMЃЌЗжБ№НЛxжсЁЂyжсгкBЁЂCСНЕуЃЎ
x+bЙ§ЕуMЃЌЗжБ№НЛxжсЁЂyжсгкBЁЂCСНЕуЃЎ
ЃЈ1ЃЉЂйЬюПеЃКЁбAЕФАыОЖЮЊЁЁ ЁЁЃЌb=ЁЁ ЁЁЃЎЃЈВЛашаДНтД№Й§ГЬЃЉ
ЂкХаЖЯжБЯпBCгыЁбAЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ2ЃЉШєEFЧаЁбAгкЕуFЗжБ№НЛABКЭBCгкGЁЂEЃЌЧвFEЁЭBCЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЃЈ3ЃЉШєЕуPдкЁбAЩЯЃЌЕуQЪЧyжсЩЯвЛЕуЧвдкЕуCЯТЗНЃЌЕБЁїPQMЮЊЕШбќжБНЧШ§НЧаЮЪБЃЌжБНгаДГіЕуQЕФзјБъЃЎ


ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПНќФъРДЃЌаТФмдДЦћГЕвдЦфЪцЪЪЛЗБЃЁЂНкФмОМУЕФгХЪЦЪмЕНШШХѕЃЌЫцжЎЖјРДЕФОЭЪЧаТФмЦћГЕЯњСПЕФМБЫйдіМгЃЌЕБЧАЪаГЁЩЯаТФмЦЏЦћГЕДгЖЏСІЩЯЗжДПЕчЖЏКЭЛьКЯЖЏСІСНжжЃЌДггУЭОЩЯгжЗжЮЊГЫгУЪНКЭЩЬгУЪНСНжжЃЌОнжаЙњЦћГЕЙЄвЕаЛсЬсЙЉЕФаХЯЂЃЌ2017ФъШЋФъаТФмдДГЫгУГЕЕФРлМЦЯњСПЮЊ57.9ЭђСОЃЌЦфжаЃЌДПЕчЖЏГЫгУГЕЯњСПЮЊ46.8ЭђСОЃЌЛьКЯЖЏСІГЫгУГЕЯњСПЮЊ11.1ЭђСОЃЛ 2017ФъШЋФъаТФмдДЩЬгУГЕЕФРлМЦЯњСПЮЊ19.8ЭђСОЃЌЦфжаЃЌДПЕчЖЏЩЬгУГЕЯњСПЮЊ18.4ЭђСОЃЌЛьКЯЖЏСІЩЬгУГЕЯњСПЮЊ1.4ЭђСОЃЌЧыИљОнвдЩЯВФСЯНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧыгУЭГМЦБэБэЪОЮвЙњ2017ФъаТФмдДЦћГЕИїРрГЕаЭЯњСПЧщПіЃЛ
ЃЈ2ЃЉаЁгБИљОнЩЯЪіаХЯЂЃЌМЦЫуГі2017ФъЮвЙњаТФмдДИїРрГЕаЭзмЯњСПЮЊ77.7ЭђСОЃЌВЂЛцжЦСЫЁА2017ФъЮвЙњаТФмдДЦћГЕЫФРрГЕаЭЯњСПБШР§ЁБЕФЩШаЮЭГМЦЭМЃЌШчЭМ1ЃЌЧыФуНЋИУЭМВЙГфЭъећЃЈЦфжаЕФАйЗжЪ§ОЋШЗЕН0.1%ЃЉЃЛ
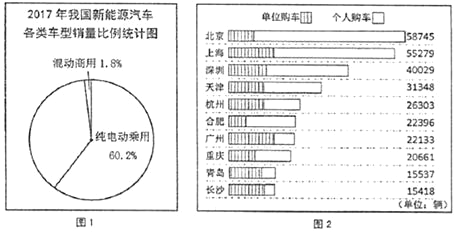
ЃЈ3ЃЉ2017ФъЮвЙњаТФмдДГЫгУГЕЯњСПзюИпЕФЪЎИіГЧЪаХХУћЧщПіШчЭМ2ЃЌЧыИљОнЭМ2жааХЯЂаДГіетаЉГЧЪааТФмдДГЫгУГЕЯњЪлЧщПіЕФЬиЕуЃЈаДГівЛЬѕМДПЩЃЉЃЛ
ЃЈ4ЃЉЪ§ОнЯдЪОЃЌ2018Фъ1ЁЋ3дТЕФаТФмдДГЫгУГЕзмЯњСПХХааАёЩЯЮЛОгЧАЫФЕФГЇМвЪЧБШбЧЕЯЁЂББЦћЁЂЩЯЦћЁЂНзМЃЌВЮМгЩчЛсЪЕМљЕФДѓбЇЩњаЁЭѕЯыЖдЦфжаСНИіГЇМвНјааЩюШыЕїбаЃЌЫћНЋЫФИіЭъШЋЯрЭЌЕФЦЙХвЧђНјааБрКХЃЈгУЁА1ЃЌ2ЃЌ3ЃЌ4ЁБвРДЮЖдгІЩЯЪіЫФИіГЇМвЃЉЃЌВЂНЋЦЙХвЧђЗХШыВЛЭИУїЕФДќзгжаНСдШЃЌДгжавЛДЮФУГіСНИіЦЙХвЧђЃЌИљОнЦЙХвЧђЩЯЕФБрКХОіЖЈвЊЕїбаЕФГЇМвЃЎЧѓаЁЭѕЧЁКУЕїбаЁАБШбЧЕЯЁБКЭЁАНЛДЁБетСНИіГЇМвЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКШчЙћвЛЬѕЯпЖЮНЋвЛИіШ§НЧаЮЗжГЩ2ИіаЁЕШбќШ§НЧаЮЃЌЮвУЧАбетЬѕЯпЖЮНазіетИіШ§НЧаЮЕФЁАКУЯпЁБЃКШчЙћСНЬѕЯпЖЮНЋвЛИіШ§НЧаЮЗжГЩ3ИіаЁЕШбќШ§НЧаЮЃЌЮвУЧАбетСНЬѕЯпЖЮНазіетИіШ§НЧаЮЕФЁАКУКУЯпЁБ.
РэНтЃК
ЃЈ1ЃЉШчЭМ1ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() БпЩЯЃЌЧв
БпЩЯЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФДѓаЁЃЛ
ЕФДѓаЁЃЛ
ЃЈ2ЃЉдкЭМ1жаЙ§Еу![]() зївЛЬѕЯпЖЮ
зївЛЬѕЯпЖЮ![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФЁАКУКУЯпЁБЃЛ
ЕФЁАКУКУЯпЁБЃЛ
дкЭМ2жаЛГіЖЅНЧЮЊ![]() ЕФЕШбќШ§НЧаЮЕФЁАКУКУЯпЁБЃЌВЂБъзЂУПИіЕШбќШ§НЧаЮЖЅНЧЕФЖШЪ§ЃЈЛГівЛжжМДПЩЃЉЃЛ
ЕФЕШбќШ§НЧаЮЕФЁАКУКУЯпЁБЃЌВЂБъзЂУПИіЕШбќШ§НЧаЮЖЅНЧЕФЖШЪ§ЃЈЛГівЛжжМДПЩЃЉЃЛ
гІгУЃК
ЃЈ3ЃЉдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() КЭ
КЭ![]() ЪЧ
ЪЧ![]() ЕФЁАКУКУЯпЁБЃЌЕу
ЕФЁАКУКУЯпЁБЃЌЕу![]() дк
дк![]() БпЩЯЃЌЕу
БпЩЯЃЌЕу![]() дк
дк![]() БпЩЯЃЌЧв
БпЩЯЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌЧыЧѓГі
ЃЌЧыЧѓГі![]() ЕФЖШЪ§.
ЕФЖШЪ§.

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com