
����Ŀ��ֱ������ϵ�У���֪A��1��0�����Ե�AΪԲ�Ļ�Բ����M��4��4���ڡ�A�ϣ�ֱ��y=��![]() x+b����M���ֱ�x�ᡢy����B��C���㣮
x+b����M���ֱ�x�ᡢy����B��C���㣮
��1������գ���A�İ뾶Ϊ�� ����b=�� ����������д�����̣�
���ж�ֱ��BC���A��λ�ù�ϵ����˵�����ɣ�
��2����EF�С�A�ڵ�F�ֱ�AB��BC��G��E����FE��BC����![]() ��ֵ��
��ֵ��
��3������P�ڡ�A�ϣ���Q��y����һ�����ڵ�C�·�������PQMΪ����ֱ��������ʱ��ֱ��д����Q�����꣮


���𰸡�(1) 5��7;(2) ����,���ɼ�����;(3) Q�������ǣ�0��0����0��2����0����8����0��3��![]() ����
����
��������
��1��������AM����M��MQ��x����Q�����AQ��QM�����ݹ��ɶ������AM���ɣ���M������������ʽ�����b���ɣ������B��C�����֤꣬��AQM����BQM���ƣ��Ƴ���MAQ=��BMQ���Ƴ���AMB=90�����ɣ�
��2����EG=a�����ݹ��ɶ������BC��AC��CM��ֵ��������BEG����BOC���ƣ����BE��ֵ��������BEG����AFG���ƣ����GF��ֵ������BC=BE+EM+CM���������a���ɣ�
��3��������������ٵ���PQM=90��ʱ��MQ=PQ��������Գƣ��ó�Q��O�غϣ��������Q�����ꣻ�ڵ���PMQ=90�㣬MQ=MP����MD��x��MH��y��֤��MHQ�ա�MDP���Ƴ�P��Բ��x�����ύ�㣬��������𰸣��۵���QPM=90��ʱ���������������һ�����P��y������P��m��n����Q��0��b���ó����̢�4-m=n-b����4-n=-m������1-m��2+n2=52���ⷽ���鼴�����b���ڶ������P��y���ҷ���ͬ�������b��ֵ��
��1���ٽ⣺����AM����M��MQ��x����Q��

��AQ=4��1=3��MQ=4��
�ɹ��ɶ����ã�AM=![]() =5��
=5��
��M��4��4������y=��![]() x+b�ã�4=��
x+b�ã�4=��![]() ��4+b��
��4+b��
��b=7��
�ʴ�Ϊ��5��7��
�ڽ⣺���У�
�����ǣ�����AF��

y=��![]() x+7��
x+7��
��x=0ʱ��y=7����C��0��7����OC=7��
��y=0ʱ��0=��![]() x+7��
x+7��
��x=![]() ��
��
��B��![]() ��0����OB=
��0����OB=![]() ��
��
��BQ=OB��OQ=![]() ��4=
��4=![]() ��AQ=4��1=3��MQ=4��
��AQ=4��1=3��MQ=4��
��![]() =
=![]() =
=![]() ��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
�ߡ�MQA=��MQB��
���AMQ�ס�MBQ��
���MAQ=��BMQ��
�ߡ�MAQ+��AMQ=90�㣬
���AMQ+��BMQ=90�㣬
��AM��BC��
��ֱ��BC���A��λ�ù�ϵ�����У�
��2���⣺����AC��

����COB�У��ɹ��ɶ����ã�BC=![]() =
=![]() ��
��
ͬ��AC=5![]() ��
��
��AM=5���ɹ��ɶ����ã�CM=5��
��EG=a��
��EF��BC��
���FEB=��COB=90�㣬
�ߡ�OBC=��OBC��
���BEG�ס�BOC��
��![]() ��
��
��![]() =
=![]() ��
��
��BE=![]() a��
a��
��������߳������ã�EM=EF=BC��BE��CM=![]() ��
��![]() a��5��
a��5��
��EF��CB��AF��EF��
��AF��BC��
���AFG�ס�BEG��
��![]() =
=![]() ��
��
��![]() =
=![]() ��
��
��FG=![]() ��
��
��BE+EM+CM=BC��
��![]() a+a+
a+a+![]() +5=
+5=![]() ��
��
a=![]() ��
��
EG=![]() ��FG=
��FG=![]() ��
��
��![]() =
=![]() =3��
=3��
��3���⣺�ٵ���PQM=90��ʱ��MQ=PQ���ɶԳ���M��P����X��Գƣ�
����Q��O�غ���Q��0��0����
�ڵ���PMQ=90�㣬MQ=MP����MD��x��MH��y��
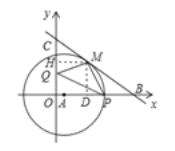
�ɵ���MHQ�ա�MDP��
��P��Բ��x�����ύ��
�Ӷ�Q��0��2����
�۵���QPM=90��ʱ�������������
��һ�����P��y������ͼ��

��P��m��n����Q��0��b���ɵã�
��4��m=n��b����4��n=��m������1��m��2+n2=52��
�ⷽ����ã�b=2��b=��8��b=2Ҳ�����������������bͬ����ֱ�Dz�ͬ����
�ڶ������P��y���ҷ���ͬ���ã�
��m��4=n��b����4��n=m������1��m��2+n2=52��
�ⷽ����ã�b=3+![]() ���ᣩ��b=3��
���ᣩ��b=3��![]() ��
��
�ۺ�������Q�������ǣ�0��0����0��2����0����8����0��3��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����Rt��ABC�У���C=90������A=30����AB���е�D��BC�߾���Ϊ3 cm������AC���ҵ�E��ʹBE+EDֵ��С����BE+ED����Сֵ��________cm.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
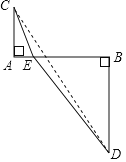
����Ŀ����ͼ����ABC�͡�DEC���ǵ���ֱ�������Σ���ACB=��DCE=90�㣬E���߶�AC�ϣ�����AD�� BE���ӳ��߽�AD��F��
��1�������߶�BE��AD��������ϵ��λ�ù�ϵ��_______________������֤������
��2������EΪ��ABC�ڲ�һ��ʱ��ʹ��D�͵�E�ֱ���AC�����࣬�����������䣮
��������ͼ2�в�ȫͼ�Σ�
�ڣ�1���н��۳���������������֤����������������˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ƽ��ֱ������ϵ�У�������y=ax2+bx+c(a��0)����A��-1��0����B��3��0����C��0��3�����㣬�䶥��ΪD������BD�������߶�BD��һ�����㣨����B��D�غϣ�������P��y��Ĵ��ߣ�����ΪE������BE��
��1���������ߵĽ���ʽ����д������D�����ꣻ
��2�����P�������Ϊ��x��y������PBE�����Ϊ����S��x�ĺ�����ϵʽ��д���Ա���x��ȡֵ��Χ�������S�����ֵ��
��3���ڣ�2���������£���Sȡ�����ֵʱ������P��x�Ĵ��ߣ�����ΪF������EF������PEF��ֱ��EF�۵�����P�Ķ�Ӧ��ΪP������ֱ��д��P�������꣬���жϵ�P���Ƿ��ڸ��������ϣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����OΪ��ABC�����Բ��AB=AC��ֱ��MN���O�����ڵ�C����BD��MN��AC��BD�ཻ�ڵ�E��

��1����֤����ABE �� ��ACD��
��2����AB = 5��BC = 3����AE��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���֪��BAC��45����AD��BC��D���ֱ���AB��ACΪ�Գ��ᣬ������ABD����ACD����Գ�ͼ�Σ�D��ĶԳƵ�ΪE��F���ӳ�EB��FC�ཻ��G�㣬�õ�������AEGF(AE��EG��GF��AF,![]() ��EAF����E����F����G=90��)��
��EAF����E����F����G=90��)��

(1) ��AD��6��BD��2����CG�ij���
(2) ��BG��a,CG��b,BC��c.
��AE=_______.(��a��b��c��ʾ)
�����������������֤���ɶ���![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ѧ�е���������ϣ�Ҳ����������о�����������һ�������¿��Ի���ת��.���ν�Ͼ��ǰѳ������ѧ���ԡ�������ϵ��ֱ�۵ļ���ͼ�Ρ�λ�ù�ϵ���������ͨ������������������������������ͨ������˼ά������˼ά�Ľ�ϣ�����ʹ���������������������廯���Ӷ����Ż�����;����Ŀ��.
(1) ��˼��Ӧ�ã���֪m�� n��Ϊ��ʵ������m+n=2��![]() ����Сֵͨ����������˼����С���뵽����������Ĺ�����������:��ͼ�� AB=2��AC=1��BD=2��AC��AB��BD��AB����E���߶�AB�ϵĶ��㣬�Ҳ���˵��غϣ�����CE��DE����AE=m�� BE=n.
����Сֵͨ����������˼����С���뵽����������Ĺ�����������:��ͼ�� AB=2��AC=1��BD=2��AC��AB��BD��AB����E���߶�AB�ϵĶ��㣬�Ҳ���˵��غϣ�����CE��DE����AE=m�� BE=n.
���ú�m�Ĵ���ʽ��ʾCE=_______�� �ú�n�Ĵ���ʽ��ʾDE= ;
�ھݴ���![]() ����Сֵ;
����Сֵ;
(2)�����Ӧ�ã����������ķ����������ʽ![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���ACB��90�㣬BC��a��AC��b��AB��c����Rt��ABC�Ƶ�O������ת90�㡢180���270�㣬���ɵ�ͼ����ͼ��ʾ����ͼ���ҹ��Ŵ���ѧ����ˬ�����ġ�����Բ��ͼ����Ҳ����������ˬ��ͼ���������ҹ�����Թ��ɶ���֤���ļ��أ�Ҳ��Ϊ��2002���ڱ����ٿ��Ĺ�����ѧ�Ҵ��Ļ����Ƶ���Ҫ���ݣ�

��1�����������ͼ��֤�����ɶ�����
��2�����������ͼ��˵��a2��b2��2ab����˵���Ⱥų�����������
��3������ݣ�2���Ľ��۽����������⣺��Ϊx����Ϊy�ij����Σ����ܳ�Ϊ8����x��yȡ��ֵʱ���ó����ε��������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
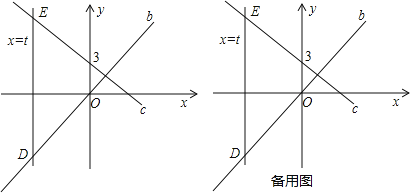
����Ŀ����ͼ����ֱ֪��c��ֱ��b����ڵ�![]() ��ֱ��c����
��ֱ��c����![]() ƽ����y��Ķ�ֱ��a�Ľ���ʽΪ
ƽ����y��Ķ�ֱ��a�Ľ���ʽΪ![]() ���Ҷ�ֱ��a�ֱ�ֱ��b��c�ڵ�D��
���Ҷ�ֱ��a�ֱ�ֱ��b��c�ڵ�D��![]() ��D���Ϸ�
��D���Ϸ�![]() ��
��
![]() ��ֱ��b��ֱ��c�Ľ���ʽ��
��ֱ��b��ֱ��c�Ľ���ʽ��
![]() ��P��y����һ�����㣬������
��P��y����һ�����㣬������![]() �ǵ���ֱ�������Σ����P�����꣮
�ǵ���ֱ�������Σ����P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com