
【题目】在Rt△ABC中,∠ACB=90°,BC=a,AC=b,AB=c.将Rt△ABC绕点O依次旋转90°、180°和270°,构成的图形如图所示.该图是我国古代数学家赵爽制作的“勾股圆方图”,也被称作“赵爽弦图”,它是我国最早对勾股定理证明的记载,也成为了2002年在北京召开的国际数学家大会的会标设计的主要依据.

(1)请利用这个图形证明勾股定理;
(2)请利用这个图形说明a2+b2≥2ab,并说明等号成立的条件;
(3)请根据(2)的结论解决下面的问题:长为x,宽为y的长方形,其周长为8,求当x,y取何值时,该长方形的面积最大?最大面积是多少?
【答案】(1)详见解析;(2)当且仅当a=b时,等号成立;(3)当且仅当x=y=2时,长方形的面积最大,最大面积是4.
【解析】
1)根据题意,我们可在图中找等量关系,由中间的小正方形的面积等于大正方形的面积减去四个直角三角形的面积,列出等式化简即可得出勾股定理的表达式.
(2)利用非负数的性质证明即可.
(3)利用(2)中的结论求得当x,y取何值时,该矩形面积最大以及其最大面积.
解:(1)因为边长为c的正方形面积为c2,
它也可以看成是由4个直角三角形与1个边长为(a– b)的小正方形组成的,
它的面积为4×![]() ab+(a– b)2=a2+b2,
ab+(a– b)2=a2+b2,
所以c2=a2+b2.
(2)∵(a– b)2≥0,
∴a2+b2–2ab≥0,∴a2+b2≥2ab,
当且仅当a=b时,等号成立.
(3)依题意得2(x+y)=8,∴x+y=4,长方形的面积为xy,
由(2)的结论知2xy≤x2+y2=(x+y)2–2xy,
∴4xy≤(x+y)2,∴xy≤4,
当且仅当x=y=2时,长方形的面积最大,最大面积是4.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,E为AC的中点,AD平分∠BAC,BA:CA=2:3,AD与BE相交于点O,若△OAE的面积比△BOD的面积大1,则△ABC的面积是( )

A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角坐标系中,已知A(1,0),以点A为圆心画圆,点M(4,4)在⊙A上,直线y=﹣![]() x+b过点M,分别交x轴、y轴于B、C两点.
x+b过点M,分别交x轴、y轴于B、C两点.
(1)①填空:⊙A的半径为 ,b= .(不需写解答过程)
②判断直线BC与⊙A的位置关系,并说明理由.
(2)若EF切⊙A于点F分别交AB和BC于G、E,且FE⊥BC,求![]() 的值.
的值.
(3)若点P在⊙A上,点Q是y轴上一点且在点C下方,当△PQM为等腰直角三角形时,直接写出点Q的坐标.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,新能源汽车以其舒适环保、节能经济的优势受到热捧,随之而来的就是新能汽车销量的急速增加,当前市场上新能漂汽车从动力上分纯电动和混合动力两种,从用途上又分为乘用式和商用式两种,据中国汽车工业协会提供的信息,2017年全年新能源乘用车的累计销量为57.9万辆,其中,纯电动乘用车销量为46.8万辆,混合动力乘用车销量为11.1万辆; 2017年全年新能源商用车的累计销量为19.8万辆,其中,纯电动商用车销量为18.4万辆,混合动力商用车销量为1.4万辆,请根据以上材料解答下列问题:
(1)请用统计表表示我国2017年新能源汽车各类车型销量情况;
(2)小颖根据上述信息,计算出2017年我国新能源各类车型总销量为77.7万辆,并绘制了“2017年我国新能源汽车四类车型销量比例”的扇形统计图,如图1,请你将该图补充完整(其中的百分数精确到0.1%);
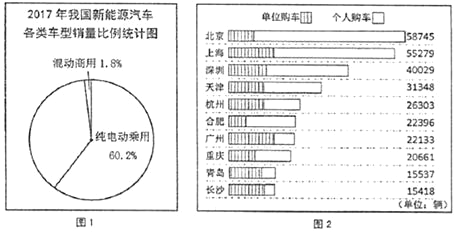
(3)2017年我国新能源乘用车销量最高的十个城市排名情况如图2,请根据图2中信息写出这些城市新能源乘用车销售情况的特点(写出一条即可);
(4)数据显示,2018年1~3月的新能源乘用车总销量排行榜上位居前四的厂家是比亚迪、北汽、上汽、江准,参加社会实践的大学生小王想对其中两个厂家进行深入调研,他将四个完全相同的乒乓球进行编号(用“1,2,3,4”依次对应上述四个厂家),并将乒乓球放入不透明的袋子中搅匀,从中一次拿出两个乒乓球,根据乒乓球上的编号决定要调研的厂家.求小王恰好调研“比亚迪”和“江淮”这两个厂家的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知动点A在函数y=![]() (x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于___.
(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,共享单车服务的推出(如图1),极大的方便了城市公民绿色出行,图2是某品牌某型号单车的车架新投放时的示意图(车轮半径约为30cm),其中BC∥直线l,∠BCE=71°,CE=54cm.
(1)求单车车座E到地面的高度;(结果精确到1cm)
(2)根据经验,当车座E到CB的距离调整至等于人体胯高(腿长)的0.85时,坐骑比较舒适.小明的胯高为70cm,现将车座E调整至座椅舒适高度位置E′,求EE′的长.(结果精确到0.1cm)
(参考数据:sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一条线段将一个三角形分成2个小等腰三角形,我们把这条线段叫做这个三角形的“好线”:如果两条线段将一个三角形分成3个小等腰三角形,我们把这两条线段叫做这个三角形的“好好线”.
理解:
(1)如图1,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 边上,且
边上,且![]() ,求
,求![]() 的大小;
的大小;
(2)在图1中过点![]() 作一条线段
作一条线段![]() ,使
,使![]() ,
,![]() 是
是![]() 的“好好线”;
的“好好线”;
在图2中画出顶角为![]() 的等腰三角形的“好好线”,并标注每个等腰三角形顶角的度数(画出一种即可);
的等腰三角形的“好好线”,并标注每个等腰三角形顶角的度数(画出一种即可);
应用:
(3)在![]() 中,
中,![]() ,
,![]() 和
和![]() 是
是![]() 的“好好线”,点
的“好好线”,点![]() 在
在![]() 边上,点
边上,点![]() 在
在![]() 边上,且
边上,且![]() ,
,![]() ,请求出
,请求出![]() 的度数.
的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com