
����Ŀ����ͼ�٣���ABC�У�AB=AC����B����C��ƽ���߽���O�㣬��O����EF��BC��AB��AC��E��F.
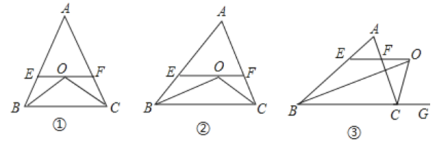
(1)ͼ�����м�������������?����:EF��BE��CF֮���������Ĺ�ϵ.
(2)��ͼ��,��AB��AC�������������䣬ͼ�л��е�����������?����У��ֱ�ָ������.�ڵ�(1)����EF��BE��CF��Ĺ�ϵ��������?
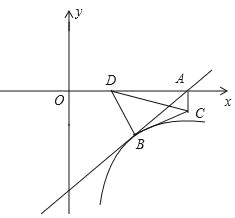
(3)��ͼ�ۣ�����ABC�С�B��ƽ����BO�����������ƽ����CO����O����O����OE��BC��AB��E����AC��F.��ʱͼ�л��е�����������?EF��BE��CF��ϵ�����?˵���������.
���𰸡���1����AEF����OEB����OFC����OBC����ABC��5����EF=BE+FC����2���У���EOB����FOC�����ڣ���3���У�EF=BE-FC��
��������
��1����AB=AC���ɵá�ABC=��ACB������֪OB��OC�ֱ�ƽ�֡�ABC����ACB���ʡ�EBO=��OBC=��FCO=��OCB������EF��BC���ɵã���OEB=��OBC=��EBO����FOC=��FCO=��BCO���ɴ˿ɵó��ĵ����������У���AEF����OEB����OFC����OBC����ABC��
��֪�ˡ�EOB�͡�FOC�ǵ��������Σ���EO=BE��OF=FC����EF=BE+FC��
��2���ɣ�1����֤�����̿�֪����֤��OEB����OFC�ǵ��������εĹ����У���AB=AC������û�й�ϵ�������������������λ����������ԣ�1���еó���EF=BE+FC�Ľ����Գ�����
��3��˼·�루2����ͬ��ֻ������������EF=BE-FC��
�⣺��1��ͼ���ǵ��������ε��У���AEF����OEB����OFC����OBC����ABC��
EF��BE��FC�Ĺ�ϵ��EF=BE+FC���������£�
��AB=AC��
���ACB=��ABC����ABC�ǵ��������Σ�
��BO��CO�ֱ�ƽ�֡�ABC�͡�ACB��
���ABO=��OBC=![]() ��ABC����OCB=��ACO=
��ABC����OCB=��ACO=![]() ��ACB��
��ACB��
��EF��BC��
���EOB=��OBC����FOC=��OCB��
���ABO=��OBC=��EOB=��OCB=��FOC=��FCO��
���EOB����OBC����FOC���ǵ��������Σ�
��EF��BC��
���AEF=��ABC����AFE=��ACB��
���AEF=��AFE��
���AEF�ǵ��������Σ�
��OB��OCƽ�֡�ABC����ACB��
���ABO=��OBC����ACO=��OCB��
��EF��BC��
���EOB=��OBC=��EBO����FOC=��OCB=��FCO��
��EO=EB��FO=FC��
��EF=EO+OF=BE+CF��
��2����AB��ACʱ����EOB����FOC��Ϊ���������Σ���1���Ľ�����Ȼ������
��OB��OCƽ�֡�ABC����ACB��
���ABO=��OBC����ACO=��OCB��
��EF��BC��
���EOB=��OBC=��EBO����FOC=��OCB=��FCO��
��EO=EB��FO=FC��
��EF=EO+OF=BE+CF��
��3����EOB�͡�FOC���ǵ��������Σ�EF=BE-FC���������£�
ͬ��1����֤�á�EOB�ǵ��������Σ�
��EO��BC��
���FOC=��OCG��
��OCƽ�֡�ACG��
���ACO=��FOC=��OCG��
��FO=FC���ʡ�FOC�ǵ��������Σ�
��EF=EO-FO=BE-FC��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�˳а���һ��������,�������һ���������.���������ϳ����Ķ��Ӱ�æ.�������������������������������60����,��ÿ���㶼���ϱ��,�Ż�����;����2��,���������״������ڴ�������50����,���������2������ǵ�.���赱ʱ������������Ϊ2.8Ԫ/��,ƽ��ÿ�������2.3��,���ܰ���������һ�½�������������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У�AB��AC����DΪBC��һ�㣬��DA��DB����ʱ��ACDҲǡ��Ϊ���������Σ����BAC��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
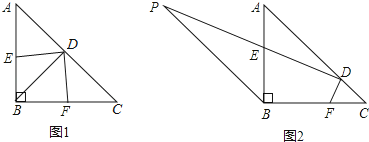
����Ŀ���ڵ���������ABC�У���ABC��90�ȣ�D��AC���ϵĶ��㣬����BD��E��F�ֱ���AB��BC�ϵĵ㣬��DE��DF������1����ͼ1����DΪAC���ϵ��е㣮
��1����գ���C���� ������DBC���� ����
��2����֤����BDE�ա�CDF��
��3����ͼ2��D�ӵ�C��������E��PD�ϣ���ÿ��1����λ���ٶ����յ�A�˶�������B��BP��AC����PB��AC��4����E��PD�ϣ����D�˶���ʱ��Ϊt�루0��1��4���ڵ�D�˶��Ĺ����У�ͼ���ܷ����ȫ�������Σ����ܣ���ֱ��д��t��ֵ�Լ�����Ӧ��ȫ�������εĶ����������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��BΪ���㣬��ֱ��l//AB��P��l��һ���㣮��M��N�ֱ�ΪPA��PB���е㣬�������и�ֵ��
���߶�MN�ij���
�ڡ�PAB���ܳ���
�ۡ�PMN�������
��ֱ��MN��AB֮��ľ��룻
�ݡ�APB�Ĵ�С��
���л����P���ƶ����仯���ǣ� ��

A. �ڢ� B. �ڢ� C. �٢ۢ� D. �ܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
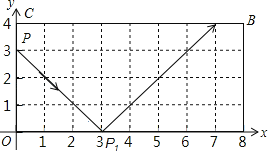
����Ŀ����ͼ������С��ӵ�P��0��3������������ʾ�����˶���ÿ��С����������OABC�ı�ʱ����������ʱ����ǵ�������ǣ���С���1���������εı�ʱ�ĵ�ΪP1����2���������εı�ʱ�ĵ�ΪP2��������n���������εı�ʱ�ĵ�ΪPn����P2019��������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ��
��![]() ����
����![]() ��
��![]() ��һ�㣮
��һ�㣮
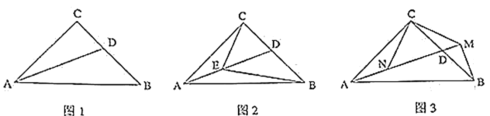
��1����ͼ![]() ��
��![]() ƽ��
ƽ��![]() ����֤��
����֤��![]() ��
��
��2����ͼ![]() ����
����![]() ���߶�
���߶�![]() �ϣ���
�ϣ���![]() ��
��![]() ����֤��
����֤��![]() ��
��
��3����ͼ![]() ��
��![]() ����
����![]() ����
����![]() ��
��![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ������
������![]() ����
����![]() ����
����![]() ��
��![]() ��
��![]() ����֤��
����֤��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=kx��10������A��12��0����B��a����5����˫����y=![]() ������B��
������B��
��1����ֱ��y=kx��10��˫����y=![]() �ĺ�������ʽ��
�ĺ�������ʽ��
��2����C�ӵ�A�������ع���A��y��ƽ�е�ֱ�������˶����ٶ�Ϊÿ��1����λ���ȣ���C���˶�ʱ��Ϊt��0��t��12��������BC����BD��BC��x���ڵ�D������CD��
������C��˫������ʱ����t��ֵ��
����0��t��6��Χ�ڣ���BCD�Ĵ�С��������仯����tan��BCD�ı仯��Χ������������仯����tan��BCD��ֵ��
����DC=![]() ʱ����ֱ��д��t��ֵ��
ʱ����ֱ��д��t��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com