
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点.
上一点.
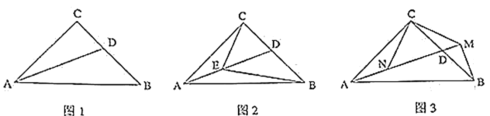
(1)如图![]() ,
,![]() 平分
平分![]() .求证:
.求证:![]() ;
;
(2)如图![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() ,
,![]() ,求证:
,求证:![]() .
.
(3)如图![]() ,
,![]() ,过
,过![]() 点作
点作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,过
,过![]() 点作
点作![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() .
.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】
(1)延长AC至E,使CE=CD,利用AAS证出△BAD≌△EAD,从而得出AB=AE,即可证出结论;
(2)过点C作CF⊥EC交AD的延长线于点F,连接BF,先利用SAS证出△ACE≌△BCF,从而证出AE=BF,∠CEA=∠CFB,再证出∠EFB=90°,利用30°所对的直角边是斜边的一半即可证出结论;
(3)过点C作CE⊥AM于M,先利用AAS证出△CNA≌△CMB,即可证出CN=CM,根据等腰三角形的性质可得NE=EM,然后利用AAS证出△CED≌△BMD,从而得出ED=DM,然后根据线段的关系即可得出结论.
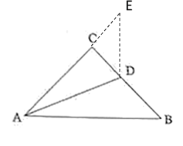
解:(1)延长AC至E,使CE=CD
∵![]() ,
,![]()
∴∠ECD=180°-∠ACB=90°,∠B=∠CAB=![]() (180°-∠ACB)=45°
(180°-∠ACB)=45°
∴△CDE为等腰三角形
∴∠E=45°
∴∠B=∠E
∵![]() 平分
平分![]()
∴∠BAD=∠EAD
在△BAD和△EAD中
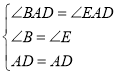
∴△BAD≌△EAD
∴AB=AE
∵AE=AC+CE=AC+CD
∴AB= AC+CD
(2)过点C作CF⊥EC交AD的延长线于点F,连接BF
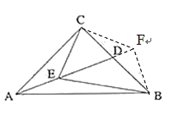
∵∠CED=45°
∴△CEF为等腰直角三角形
∴CE=CF,∠CFE=∠CEF=45°
∵△ABC为等腰直角三角形
∴∠ACB=90°,CA=CB,
∴∠ACE+∠ECB=90°,∠BCF+∠ECB=90°
∴∠ACE=∠BCF
在△ACE和△BCF中
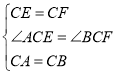
∴△ACE≌△BCF
∴AE=BF,∠CEA=∠CFB
∵∠CEA=180°-∠CEF=135°
∴∠CFB=135°
∴∠EFB=∠CFB-∠CFE=90°
在Rt△EFB中,∠BEF=30°
∴BE=2BF
∴BE=2AE
(3)过点C作CE⊥AM于M,
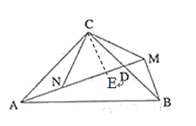
∵△ABC为等腰直角三角形
∴∠ACB=90°,CA=CB
∵CN⊥CM,BM⊥AM
∴∠NCM=90°,∠BMA=90°
∴∠ACN+∠NCB=90°,∠BCM+∠NCB=90°,
∴∠ACN=∠BCM
∴∠CNA=∠NCM+∠CMN=90°+∠CMN=∠CMB
在△CNA和△CMB中

∴△CNA≌△CMB
∴CN=CM
∴△CNM为等腰直角三角形
∴NE=EM
在△CED和△BMD中
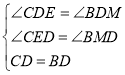
∴△CED≌△BMD
∴ED=DM
∴EM=2DM
∴NE=2DM
∴DN=NE+ED=3DM


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】我们已经学习过多项式除以单项式,多项式除以多项式一般可用竖式计算,步骤如下:
①把被除式、除式按某个字母作降幂排列,并把所缺的项用零补齐;
②用被除式的第一项除以除式第一项,得到商式的第一项;
③用商式的第一项去乘除式,把积写在被除式下面(同类项对齐),消去相等项;
④把减得的差当作新的被除式,再按照上面的方法继续演算,直到余式为零或余式的次数低于除式的次数时为止,被除式=除式×商式+余式.若余式为零,说明这个多项式能被另一个多项式整除.
例如:计算(6x4﹣7x3﹣x2﹣1)÷(2x+1),可用竖式除法如图:
所以6x4﹣7x3﹣x2﹣1除以2x+1,商式为3x3﹣5x2+2x﹣1,余式为0.
根据阅读材料,请回答下列问题(直接填空):

(1)(2x3+x﹣3)÷(x﹣1)= ;
(2)(4x2﹣4xy+y2+6x﹣3y﹣10)÷(2x﹣y+5)= ;
(3)[(x﹣2)(x﹣3)+1]÷(x﹣1)的余式为 ;
(4)x3+ax2+bx﹣15能被x2﹣2x+3整除,则a= ,b= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC交AB、AC于E、F.
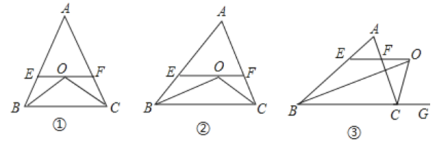
(1)图①中有几个等腰三角形?猜想:EF与BE、CF之间有怎样的关系.
(2)如图②,若AB≠AC,其他条件不变,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?
(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植4-7棵,活动结束后随机抽查了若干名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成扇形图(如图甲)和条形图(图乙),回答下列问题:
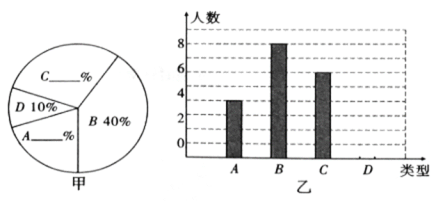
(1)求这次抽查的学生数;
(2)补全图甲和图乙;
(3)计算被抽查学生每人植树量的平均数,并估计这260名学生共植树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
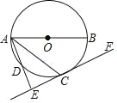
【题目】如图,AB为⊙O的直径,点C,D在⊙O上,且点C是![]() 的中点,过点 C作AD的垂线 EF交直线 AD于点 E.
的中点,过点 C作AD的垂线 EF交直线 AD于点 E.
(1)求证:EF是⊙O的切线;
(2)连接BC,若AB=5,BC=3,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,试分别根据下列条件,求出点
,试分别根据下列条件,求出点![]() 的坐标。
的坐标。
(1)点![]() 在
在![]() 轴上;
轴上;
(2)点![]() 横坐标比纵坐标大3;
横坐标比纵坐标大3;
(3)点![]() 在过
在过![]() 点,且与
点,且与![]() 轴平行的直线上。
轴平行的直线上。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,一次函数
中,一次函数![]() 的图象过点A(4,1)与正比例函数
的图象过点A(4,1)与正比例函数![]() (
(![]() )的图象相交于点B(
)的图象相交于点B(![]() ,3),与
,3),与![]() 轴相交于点C.
轴相交于点C.
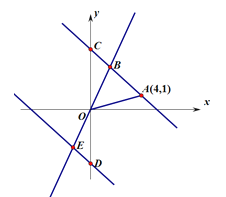
(1)求一次函数和正比例函数的表达式;
(2)若点D是点C关于![]() 轴的对称点,且过点D的直线DE∥AC交BO于E,求点E的坐标;
轴的对称点,且过点D的直线DE∥AC交BO于E,求点E的坐标;
(3)在坐标轴上是否存在一点![]() ,使
,使![]() .若存在请求出点
.若存在请求出点![]() 的坐标,若不存在请说明理由.
的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A.角平分线上的点到这个角两边的距离相等
B.角的内部到角的两边的距离相等的点在角的平分线上
C.三角形三条角平分线的交点到三条边的距离相等
D.以上均不正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com